Menu Close

Find-the-positive-integer-n-such-that-tan-1-1-3-tan-1-1-4-tan-1-1-5-tan-1-1-n-pi-4-

Tinku Tara 0 Comments
Pin




Question Number 111725 by Aina Samuel Temidayo last updated on 04/Sep/20
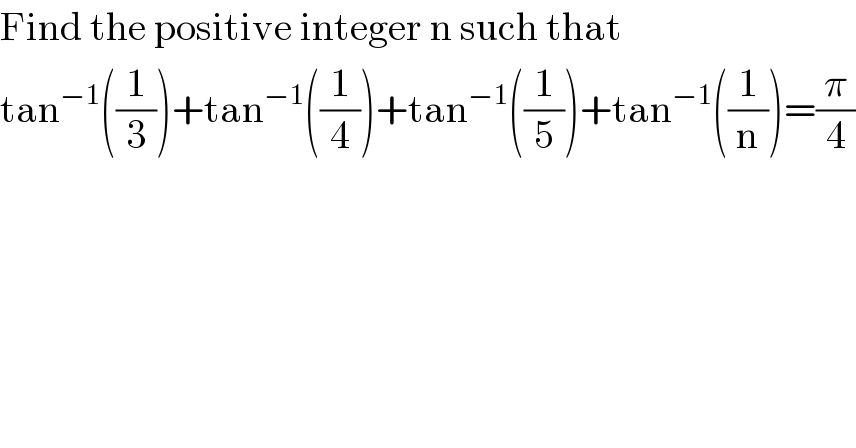
Find the positive integer n such that tan^(−1) ((1/3))+tan^(−1) ((1/4))+tan^(−1) ((1/5))+tan^(−1) ((1/n))=(π/4)
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{n}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{5}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{n}}\right)=\frac{\pi}{\mathrm{4}} \\ $$
Answered by $@y@m last updated on 04/Sep/20
Let tan^(−1) ((1/3))=α⇒tan α=(1/3) Let tan^(−1) ((1/4))=β⇒tan β=(1/4) Let tan^(−1) ((1/5))=γ⇒tan γ=(1/5) Let tan^(−1) ((1/n))=δ⇒tan δ=(1/n) ATQ, α+β+γ+δ=(π/4) α+β+γ=(π/4)−δ tan (α+β+γ)=tan ((π/4)−δ) (((1/3)+(1/4)+(1/5)−(1/(3.4.5)))/(1−(1/(3.4))−(1/(4.5))−(1/(5.3))))=((1−tan δ)/(1+tan δ)) ((1−tan δ)/(1+tan δ))=(((20+15+12−1)/(60))/((60−5−3−4)/(60)))=((46)/(48))=((23)/(24)) 24(1−tan δ)=23(1+tan δ) 1=47tan δ tan δ=(1/(47)) δ=tan^(−1) ((1/(47))) n=47
$${Let}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\alpha\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${Let}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\beta\Rightarrow\mathrm{tan}\:\beta=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${Let}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{5}}\right)=\gamma\Rightarrow\mathrm{tan}\:\gamma=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${Let}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{n}}\right)=\delta\Rightarrow\mathrm{tan}\:\delta=\frac{\mathrm{1}}{{n}} \\ $$$${ATQ}, \\ $$$$\alpha+\beta+\gamma+\delta=\frac{\pi}{\mathrm{4}} \\ $$$$\alpha+\beta+\gamma=\frac{\pi}{\mathrm{4}}−\delta \\ $$$$\mathrm{tan}\:\left(\alpha+\beta+\gamma\right)=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\delta\right) \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{4}.\mathrm{5}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}.\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{5}.\mathrm{3}}}=\frac{\mathrm{1}−\mathrm{tan}\:\delta}{\mathrm{1}+\mathrm{tan}\:\delta} \\ $$$$\frac{\mathrm{1}−\mathrm{tan}\:\delta}{\mathrm{1}+\mathrm{tan}\:\delta}=\frac{\frac{\mathrm{20}+\mathrm{15}+\mathrm{12}−\mathrm{1}}{\mathrm{60}}}{\frac{\mathrm{60}−\mathrm{5}−\mathrm{3}−\mathrm{4}}{\mathrm{60}}}=\frac{\mathrm{46}}{\mathrm{48}}=\frac{\mathrm{23}}{\mathrm{24}} \\ $$$$\mathrm{24}\left(\mathrm{1}−\mathrm{tan}\:\delta\right)=\mathrm{23}\left(\mathrm{1}+\mathrm{tan}\:\delta\right) \\ $$$$\mathrm{1}=\mathrm{47tan}\:\delta \\ $$$$\mathrm{tan}\:\delta=\frac{\mathrm{1}}{\mathrm{47}} \\ $$$$\delta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{47}}\right) \\ $$$${n}=\mathrm{47} \\ $$
Commented by Aina Samuel Temidayo last updated on 04/Sep/20
47 is part of the options I have here. Thanks.
$$\mathrm{47}\:\mathrm{is}\:\mathrm{part}\:\mathrm{of}\:\mathrm{the}\:\mathrm{options}\:\mathrm{I}\:\mathrm{have}\:\mathrm{here}. \\ $$$$\mathrm{Thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *