Question Number 33463 by NECx last updated on 17/Apr/18
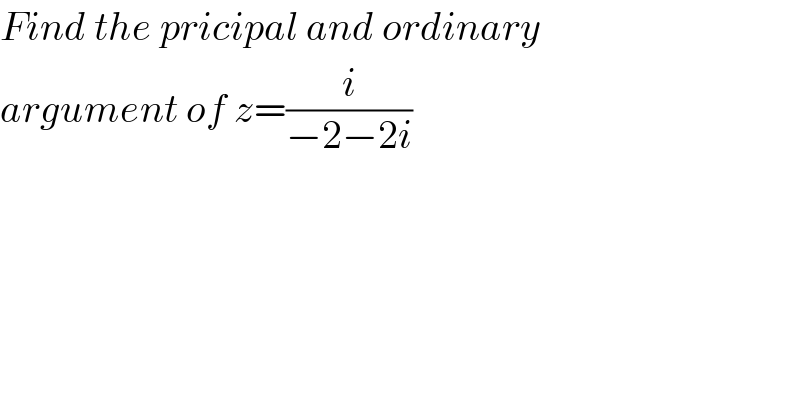
$${Find}\:{the}\:{pricipal}\:{and}\:{ordinary} \\ $$$${argument}\:{of}\:{z}=\frac{{i}}{−\mathrm{2}−\mathrm{2}{i}} \\ $$
Commented by abdo imad last updated on 17/Apr/18
![z = ((−i)/(2(1+i))) = ((−i(1−i))/4) = ((1−i)/4) ⇒∣z∣ =(1/4)∣1−i∣ =((√2)/4) z =(1/4) −(i/4) =((√2)/4)( (1/( (√2))) −(i/( (√2)))) =((√2)/2) e^(−i(π/4)) ⇒arg(z)≡−(π/4)[2π] .](https://www.tinkutara.com/question/Q33481.png)
$${z}\:=\:\frac{−{i}}{\mathrm{2}\left(\mathrm{1}+{i}\right)}\:=\:\frac{−{i}\left(\mathrm{1}−{i}\right)}{\mathrm{4}}\:=\:\frac{\mathrm{1}−{i}}{\mathrm{4}}\:\Rightarrow\mid{z}\mid\:=\frac{\mathrm{1}}{\mathrm{4}}\mid\mathrm{1}−{i}\mid\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$${z}\:=\frac{\mathrm{1}}{\mathrm{4}}\:−\frac{{i}}{\mathrm{4}}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left(\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:{e}^{−{i}\frac{\pi}{\mathrm{4}}} \:\Rightarrow{arg}\left({z}\right)\equiv−\frac{\pi}{\mathrm{4}}\left[\mathrm{2}\pi\right]\:. \\ $$
