Question Number 29320 by Glorious Man last updated on 07/Feb/18
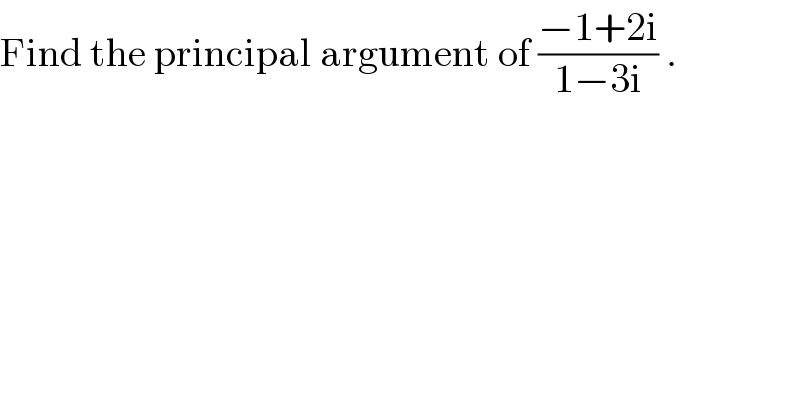
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{principal}\:\mathrm{argument}\:\mathrm{of}\:\frac{−\mathrm{1}+\mathrm{2i}}{\mathrm{1}−\mathrm{3i}}\:. \\ $$
Commented by abdo imad last updated on 08/Feb/18
![∣−1+2i∣=(√5) and −1+2i=(√5)(((−1)/( (√5))) +i(2/( (√5))))=r e^(iθ) ⇒ r=(√5) and cosθ= ((−1)/( (√5))) and sinθ =(2/( (√5))) ⇒tanθ =−2 ⇒θ=−actan2 ∣1−3i∣=(√(10)) and 1−3i=(√(10))((1/( (√(10)))) −(3/( (√(10)))) i)=r e^(iϕ) ⇒ r=(√(10)) and cosϕ =(1/( (√(10)))) and sinϕ=−(3/( (√(10)))) ⇒tanϕ=−3 ⇒ ϕ=−arctan3 so Arg(((−1+2i)/(1−3i)))≡θ −ϕ [2π] ≡ arctan3 −arctan2 [2π] .](https://www.tinkutara.com/question/Q29357.png)
$$\mid−\mathrm{1}+\mathrm{2}{i}\mid=\sqrt{\mathrm{5}}\:{and}\:−\mathrm{1}+\mathrm{2}{i}=\sqrt{\mathrm{5}}\left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:+{i}\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\right)={r}\:{e}^{{i}\theta} \Rightarrow \\ $$$${r}=\sqrt{\mathrm{5}}\:{and}\:{cos}\theta=\:\frac{−\mathrm{1}}{\:\sqrt{\mathrm{5}}}\:{and}\:{sin}\theta\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\:\Rightarrow{tan}\theta\:=−\mathrm{2} \\ $$$$\Rightarrow\theta=−{actan}\mathrm{2} \\ $$$$\mid\mathrm{1}−\mathrm{3}{i}\mid=\sqrt{\mathrm{10}}\:\:{and}\:\mathrm{1}−\mathrm{3}{i}=\sqrt{\mathrm{10}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}\:−\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}\:{i}\right)={r}\:{e}^{{i}\varphi} \\ $$$$\Rightarrow\:{r}=\sqrt{\mathrm{10}}\:{and}\:{cos}\varphi\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}\:{and}\:{sin}\varphi=−\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}} \\ $$$$\Rightarrow{tan}\varphi=−\mathrm{3}\:\Rightarrow\:\varphi=−{arctan}\mathrm{3}\:{so}\: \\ $$$${Arg}\left(\frac{−\mathrm{1}+\mathrm{2}{i}}{\mathrm{1}−\mathrm{3}{i}}\right)\equiv\theta\:−\varphi\:\left[\mathrm{2}\pi\right]\:\equiv\:{arctan}\mathrm{3}\:−{arctan}\mathrm{2}\:\left[\mathrm{2}\pi\right]\:. \\ $$
