Question Number 60734 by Tawa1 last updated on 25/May/19
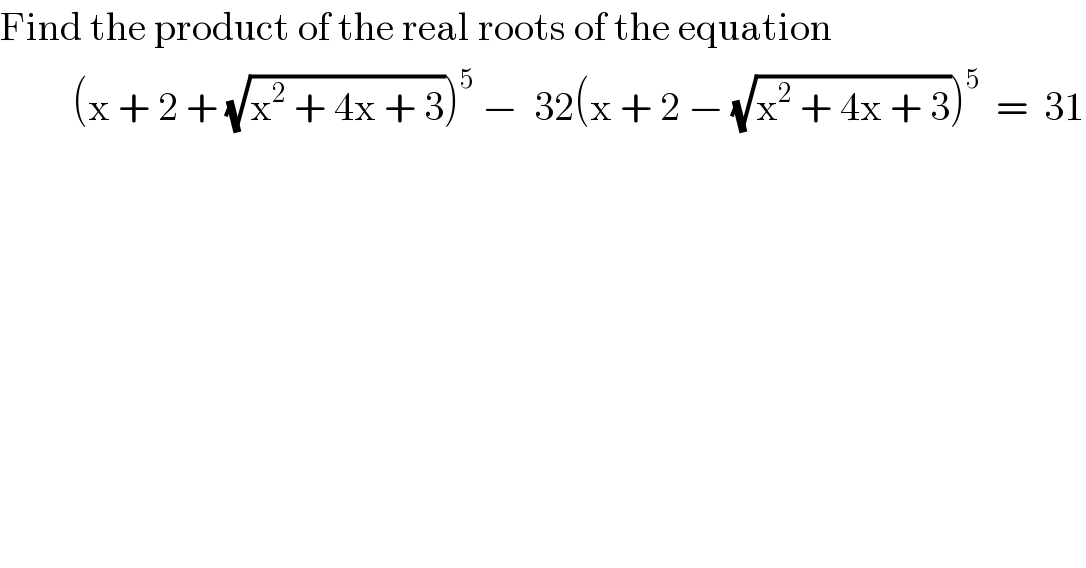
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{product}\:\mathrm{of}\:\mathrm{the}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{x}\:+\:\mathrm{2}\:+\:\sqrt{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{4x}\:+\:\mathrm{3}}\right)^{\mathrm{5}} \:−\:\:\mathrm{32}\left(\mathrm{x}\:+\:\mathrm{2}\:−\:\sqrt{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{4x}\:+\:\mathrm{3}}\right)^{\mathrm{5}} \:\:=\:\:\mathrm{31} \\ $$
Commented by Prithwish sen last updated on 25/May/19
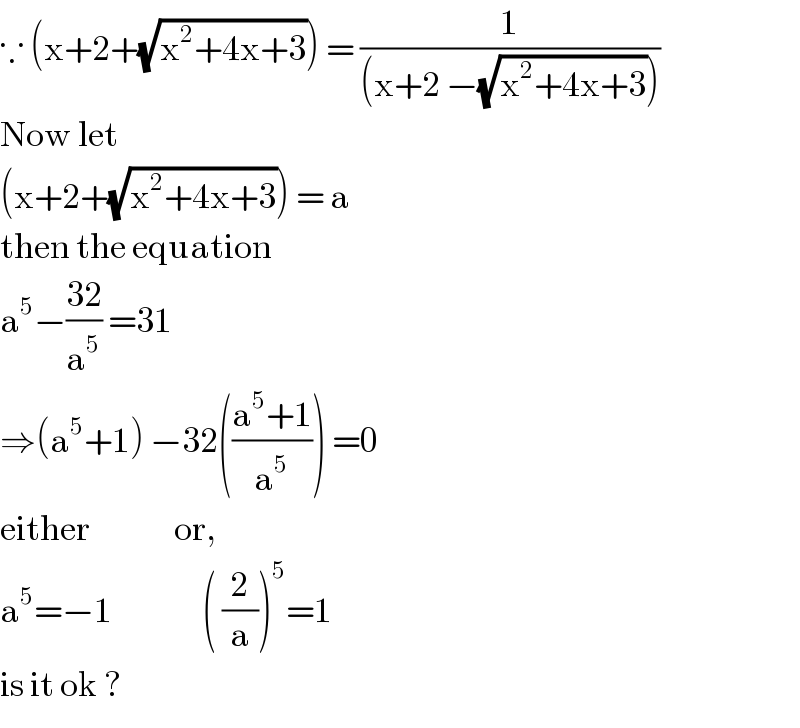
$$\because\:\left(\mathrm{x}+\mathrm{2}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{3}}\right)\:=\:\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{2}\:−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{3}}\right)} \\ $$$$\mathrm{Now}\:\mathrm{let}\: \\ $$$$\left(\mathrm{x}+\mathrm{2}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{3}}\right)\:=\:\mathrm{a} \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{a}^{\mathrm{5}} −\frac{\mathrm{32}}{\mathrm{a}^{\mathrm{5}} }\:=\mathrm{31} \\ $$$$\Rightarrow\left(\mathrm{a}^{\mathrm{5}} +\mathrm{1}\right)\:−\mathrm{32}\left(\frac{\mathrm{a}^{\mathrm{5}} +\mathrm{1}}{\mathrm{a}^{\mathrm{5}} }\right)\:=\mathrm{0} \\ $$$$\mathrm{either}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{or}, \\ $$$$\mathrm{a}^{\mathrm{5}} =−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\:\frac{\mathrm{2}}{\mathrm{a}}\right)^{\mathrm{5}} =\mathrm{1} \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{ok}\:? \\ $$
Commented by Tawa1 last updated on 25/May/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by MJS last updated on 25/May/19

$$\mathrm{great}! \\ $$$$\mathrm{my}\:\mathrm{thinking}\:\mathrm{is}\:\mathrm{too}\:\mathrm{complicated}\:\mathrm{sometimes} \\ $$
Commented by Prithwish sen last updated on 25/May/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 25/May/19

$$\left({a}+{b}\right)^{\mathrm{5}} −\mathrm{32}\left({a}−{b}\right)^{\mathrm{5}} =\mathrm{31} \\ $$$${T}_{\mathrm{1}} −\mathrm{32}{T}_{\mathrm{2}} =\mathrm{31}\:\Rightarrow\:{T}_{\mathrm{1}} =\mathrm{31}+\mathrm{32}{T}_{\mathrm{2}} \\ $$$$\mathrm{trying}\:\mathrm{some}\:\mathrm{easy}\:\mathrm{numbers}\:\mathrm{I}\:\mathrm{found}\:\mathrm{these}: \\ $$$$\left({a}+{b}\right)=−\mathrm{1}\wedge\left({a}−{b}\right)=−\mathrm{1} \\ $$$${x}+\mathrm{2}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}}=−\mathrm{1} \\ $$$$\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}}=\pm\left({x}+\mathrm{3}\right) \\ $$$$\sqrt{\left({x}+\mathrm{3}\right)\left({x}+\mathrm{1}\right)}=\pm\left({x}+\mathrm{3}\right) \\ $$$$\left({x}+\mathrm{3}\right)\left({x}+\mathrm{1}\right)=\left({x}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{x}=−\mathrm{3}\:\mathrm{in}\:\mathrm{both}\:\mathrm{cases} \\ $$$$ \\ $$$$\left({a}+{b}\right)^{\mathrm{5}} =\mathrm{32}\wedge\left({a}−{b}\right)^{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{32}} \\ $$$${x}+\mathrm{2}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}}=\sqrt[{\mathrm{5}}]{\mathrm{32}}\:\:\:\:\:{x}+\mathrm{2}−\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{5}}]{\mathrm{32}}} \\ $$$$\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}}=−{x}\:\:\:\:\:\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}}={x}+\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}={x}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}=\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${x}=−\frac{\mathrm{3}}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$$$\mathrm{of}\:\mathrm{course}\:\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{yet}\:\mathrm{know}\:\mathrm{if}\:\mathrm{there}\:\mathrm{are}\:\mathrm{more} \\ $$$$\mathrm{solutions} \\ $$
Commented by Tawa1 last updated on 25/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
