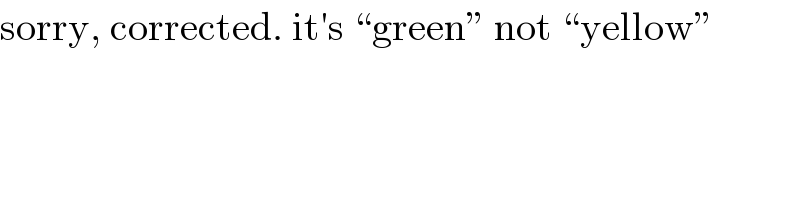Question Number 123426 by MJS_new last updated on 25/Nov/20

Commented by ajfour last updated on 25/Nov/20
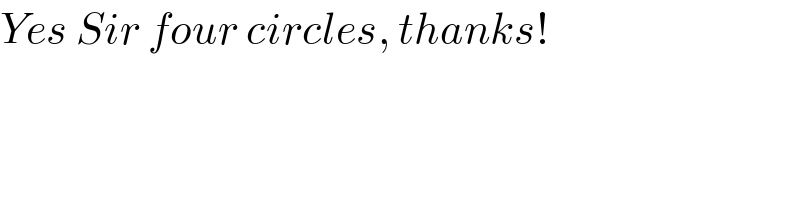
Commented by ajfour last updated on 25/Nov/20

Commented by MJS_new last updated on 25/Nov/20
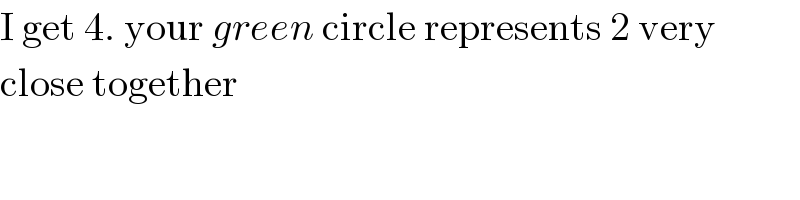
Commented by MJS_new last updated on 25/Nov/20

Commented by MJS_new last updated on 25/Nov/20