Menu Close

find-the-radius-of-S-x-n-0-x-3n-2-3n-2-2-find-the-value-of-n-0-1-3n-2-3-n-

Tinku Tara 0 Comments
Pin




Question Number 29979 by abdo imad last updated on 14/Feb/18
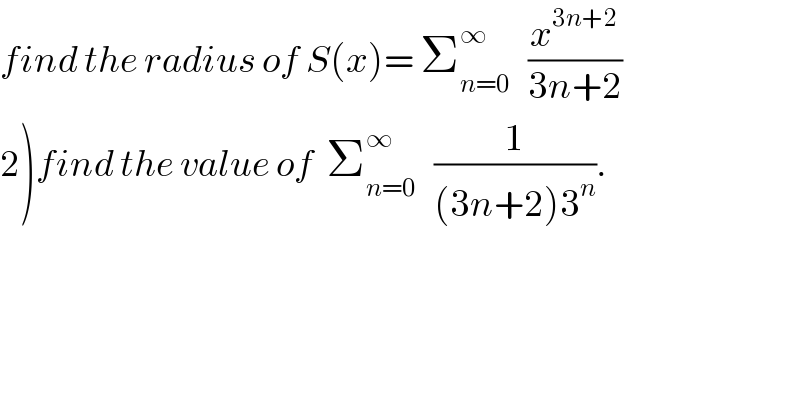
find the radius of S(x)= Σ_(n=0) ^∞ (x^(3n+2) /(3n+2)) 2)find the value of Σ_(n=0) ^∞ (1/((3n+2)3^n )).
$${find}\:{the}\:{radius}\:{of}\:{S}\left({x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{\mathrm{3}{n}+\mathrm{2}} }{\mathrm{3}{n}+\mathrm{2}} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{2}\right)\mathrm{3}^{{n}} }. \\ $$
Commented by abdo imad last updated on 17/Feb/18
1)for x=0 S(x)=0 for x≠o we have ∣((u_(n+1) (x))/(u_n (x)))∣=∣ ((x^(3n+5) /(3n+5))/(x^(3n+2) /(3n+2)))∣=((3n+2)/(3n+5)) ∣x∣_(n→∞) ^3 →∣x∣^3 ⇒if ∣x∣<1 the serie converge if ∣x∣≥1 the serie diverge if x=−1 S(−1)= Σ_(n=0) ^∞ (((−1)^n )/(3n+2)) converge(alternate serie) so R=1 2) for ∣x∣<1 and due to uniform convergence we have S^′ (x)= Σ_(n=0) ^∞ x^(3n+1) =x Σ_(n=0) ^∞ (x^3 )^n =x (1/(1−x^3 )) ⇒ S(x)= ∫ ((xdx)/(1−x^3 )) +λ let decompose F(x)= (x/(1−x^3 ))= (x/((1−x)(x^2 +x+1)))= (a/(1−x)) +((bx+c)/(x^2 +x+1)) a=lim_(x→1) (1−x)F(x)= (1/3) so F(x)= (1/(3(1−x))) +((bx+c)/(x^2 +x+1)) lim_(x→∞) xF(x)=0=((−1)/3) +b ⇒b=(1/3) ⇒ F(x)= (1/(3(1−x))) +(((1/3)x +c)/(x^2 +x+1)) F(0)=0= (1/3) +c ⇒c=−(1/3) and F(x)=(1/(3(1−x))) +(1/3) ((x−1)/(x^2 +x+1)) ⇒ ∫ (x/(1−x^3 ))dx=(1/3)( ∫ (dx/(1−x)) + ∫((x−1)/(x^2 +x+1))dx) 3 ∫ (x/(1−x^3 ))dx= ∫ (dx/(1−x)) +(1/2)∫ ((2x+1−3)/(x^2 +x+1))dx = (1/2)ln(x^2 +x+1)−ln∣1−x∣ −(3/2) ∫ (dx/(x^2 +x+1)) but ∫ (dx/(x^2 +x+1)) = ∫ (dx/((x+(1/2))^2 +(3/4))) =_(x+(1/2)=((√3)/2)t) ∫ (1/((3/4)(t^2 +1)))((√3)/2)dt =(4/3) ((√3)/2) ∫ (dt/(1+t^2 )) = (2/( (√3))) artant=(2/( (√3)))arctan((2/( (√3)))(x+(1/2))) 3 ∫ (x/(1−x^2 ))dx =ln(((√(x^2 +x+1))/(∣1−x∣)))−(√3) arctan((1/( (√3)))(2x+1)) ∫ ((xdx)/(1−x^2 )) =(1/3)ln(((√(x^2 +x+1))/(∣1−x∣))) −((√3)/3) arctan((1/( (√3)))(2x+1)) S(x)= (1/3)ln(((√(x^2 +x+1))/(∣1−x∣))) −((√3)/3) arctan((1/( (√3)))(2x+1)) +λ =A(x)+λ⇒λ=lim_(→0) S(x)−A(x)=−A(0) =((√3)/3) arctan((1/( (√3))))=((√3)/3) (π/6) =((π(√3))/(18)) and S(x)=Σ_(n=0) ^∞ (x^(3n+2) /(3n+2)) we have Σ_(n=0) ^∞ (1/((3n+2)3^n ))=Σ_(n=0) ^∞ ((((1/3))^n )/(3n+2)) =(3_(√3) )^2 Σ_(n=0) ^∞ ((((1/3_(√3) ))^(3n+2) )/(3n+2)) =(3_(√3) )^2 S(( 3_(√3) )^(−1) ) the sum S is known.
$$\left.\mathrm{1}\right){for}\:{x}=\mathrm{0}\:\:{S}\left({x}\right)=\mathrm{0}\:{for}\:{x}\neq{o}\:{we}\:{have}\: \\ $$$$\mid\frac{{u}_{{n}+\mathrm{1}} \left({x}\right)}{{u}_{{n}} \left({x}\right)}\mid=\mid\:\frac{\frac{{x}^{\mathrm{3}{n}+\mathrm{5}} }{\mathrm{3}{n}+\mathrm{5}}}{\frac{{x}^{\mathrm{3}{n}+\mathrm{2}} }{\mathrm{3}{n}+\mathrm{2}}}\mid=\frac{\mathrm{3}{n}+\mathrm{2}}{\mathrm{3}{n}+\mathrm{5}}\:\mid{x}\mid_{{n}\rightarrow\infty} ^{\mathrm{3}} \:\rightarrow\mid{x}\mid^{\mathrm{3}} \:\Rightarrow{if}\:\mid{x}\mid<\mathrm{1} \\ $$$${the}\:{serie}\:{converge}\:{if}\:\mid{x}\mid\geqslant\mathrm{1}\:{the}\:{serie}\:{diverge}\:{if}\:{x}=−\mathrm{1} \\ $$$${S}\left(−\mathrm{1}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}{n}+\mathrm{2}}\:{converge}\left({alternate}\:{serie}\right)\:{so}\:{R}=\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\:{for}\:\mid{x}\mid<\mathrm{1}\:{and}\:{due}\:{to}\:{uniform}\:{convergence}\:{we}\:{have} \\ $$$${S}^{'} \left({x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:{x}^{\mathrm{3}{n}+\mathrm{1}} ={x}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left({x}^{\mathrm{3}} \right)^{{n}} ={x}\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{3}} }\:\Rightarrow \\ $$$${S}\left({x}\right)=\:\int\:\:\frac{{xdx}}{\mathrm{1}−{x}^{\mathrm{3}} }\:+\lambda\:\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\:\frac{{x}}{\mathrm{1}−{x}^{\mathrm{3}} }=\:\frac{{x}}{\left(\mathrm{1}−{x}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}=\:\frac{{a}}{\mathrm{1}−{x}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\: \\ $$$${a}={lim}_{{x}\rightarrow\mathrm{1}} \left(\mathrm{1}−{x}\right){F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{3}}\:{so} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−{x}\right)}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$${lim}_{{x}\rightarrow\infty} \:{xF}\left({x}\right)=\mathrm{0}=\frac{−\mathrm{1}}{\mathrm{3}}\:+{b}\:\:\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{3}}\:\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−{x}\right)}\:\:+\frac{\frac{\mathrm{1}}{\mathrm{3}}{x}\:+{c}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{0}=\:\frac{\mathrm{1}}{\mathrm{3}}\:+{c}\:\Rightarrow{c}=−\frac{\mathrm{1}}{\mathrm{3}}\:{and}\: \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−{x}\right)}\:+\frac{\mathrm{1}}{\mathrm{3}}\:\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:\frac{{x}}{\mathrm{1}−{x}^{\mathrm{3}} }{dx}=\frac{\mathrm{1}}{\mathrm{3}}\left(\:\int\:\frac{{dx}}{\mathrm{1}−{x}}\:+\:\int\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}\right) \\ $$$$\mathrm{3}\:\int\:\frac{{x}}{\mathrm{1}−{x}^{\mathrm{3}} }{dx}=\:\int\:\frac{{dx}}{\mathrm{1}−{x}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2}{x}+\mathrm{1}−\mathrm{3}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)−{ln}\mid\mathrm{1}−{x}\mid\:−\frac{\mathrm{3}}{\mathrm{2}}\:\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\:{but} \\ $$$$\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:=\:\int\:\:\:\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \:\:\:\int\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{4}}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\int\:\:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{artant}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\mathrm{3}\:\int\:\:\:\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:={ln}\left(\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\mid\mathrm{1}−{x}\mid}\right)−\sqrt{\mathrm{3}}\:\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{2}{x}+\mathrm{1}\right)\right) \\ $$$$\int\:\frac{{xdx}}{\mathrm{1}−{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{3}}{ln}\left(\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\mid\mathrm{1}−{x}\mid}\right)\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{2}{x}+\mathrm{1}\right)\right) \\ $$$${S}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{3}}{ln}\left(\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{\mid\mathrm{1}−{x}\mid}\right)\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{2}{x}+\mathrm{1}\right)\right)\:+\lambda \\ $$$$={A}\left({x}\right)+\lambda\Rightarrow\lambda={lim}_{\rightarrow\mathrm{0}} \:{S}\left({x}\right)−{A}\left({x}\right)=−{A}\left(\mathrm{0}\right) \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\frac{\pi}{\mathrm{6}}\:=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{18}}\:{and}\:{S}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{3}{n}+\mathrm{2}} }{\mathrm{3}{n}+\mathrm{2}} \\ $$$${we}\:{have}\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{2}\right)\mathrm{3}^{{n}} }=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} }{\mathrm{3}{n}+\mathrm{2}} \\ $$$$=\left(\mathrm{3}_{\sqrt{\mathrm{3}}} \right)^{\mathrm{2}} \sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\left(\frac{\mathrm{1}}{\mathrm{3}_{\sqrt{\mathrm{3}}} }\right)^{\mathrm{3}{n}+\mathrm{2}} }{\mathrm{3}{n}+\mathrm{2}}\:=\left(\mathrm{3}_{\sqrt{\mathrm{3}}} \right)^{\mathrm{2}} \:{S}\left(\left(\:\mathrm{3}_{\sqrt{\mathrm{3}}} \right)^{−\mathrm{1}} \right)\:{the}\:{sum}\:{S}\:{is} \\ $$$${known}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *