Question Number 19643 by Tinkutara last updated on 13/Aug/17
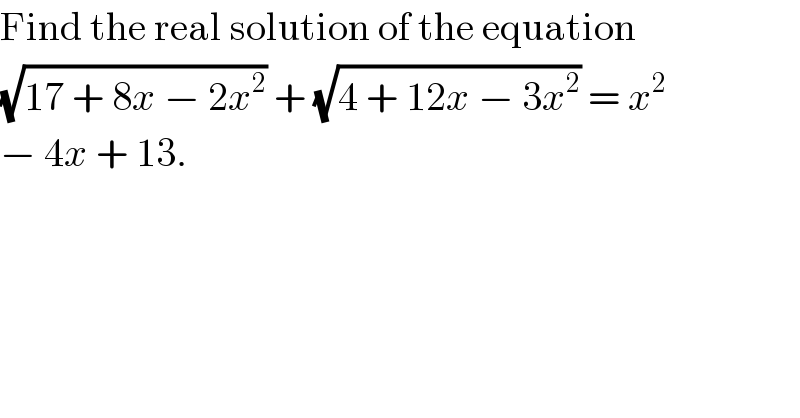
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\sqrt{\mathrm{17}\:+\:\mathrm{8}{x}\:−\:\mathrm{2}{x}^{\mathrm{2}} }\:+\:\sqrt{\mathrm{4}\:+\:\mathrm{12}{x}\:−\:\mathrm{3}{x}^{\mathrm{2}} }\:=\:{x}^{\mathrm{2}} \\ $$$$−\:\mathrm{4}{x}\:+\:\mathrm{13}. \\ $$
Answered by ajfour last updated on 13/Aug/17
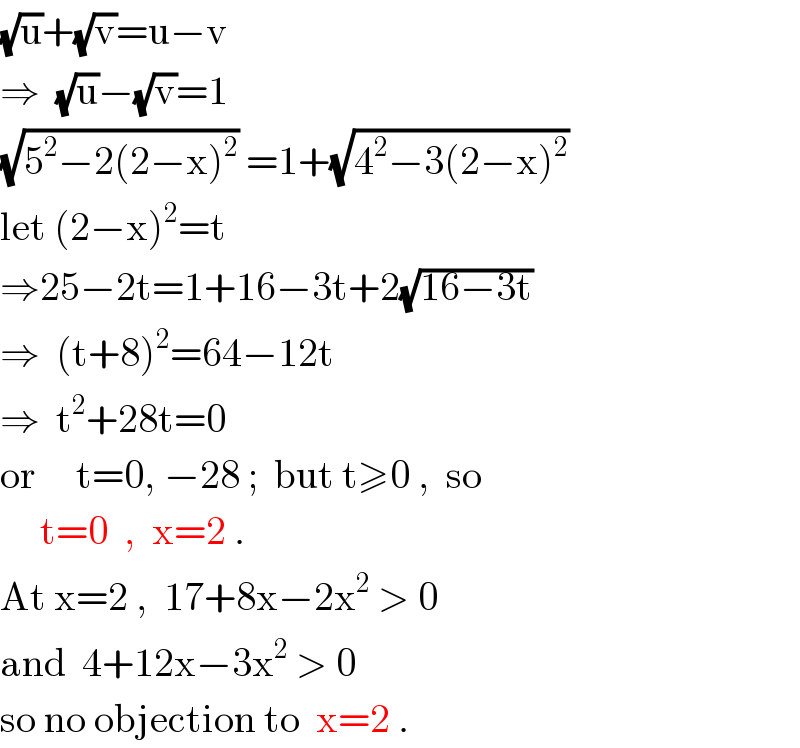
$$\sqrt{\mathrm{u}}+\sqrt{\mathrm{v}}=\mathrm{u}−\mathrm{v} \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{u}}−\sqrt{\mathrm{v}}=\mathrm{1} \\ $$$$\sqrt{\mathrm{5}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}−\mathrm{x}\right)^{\mathrm{2}} }\:=\mathrm{1}+\sqrt{\mathrm{4}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{2}−\mathrm{x}\right)^{\mathrm{2}} }\: \\ $$$$\mathrm{let}\:\left(\mathrm{2}−\mathrm{x}\right)^{\mathrm{2}} =\mathrm{t} \\ $$$$\Rightarrow\mathrm{25}−\mathrm{2t}=\mathrm{1}+\mathrm{16}−\mathrm{3t}+\mathrm{2}\sqrt{\mathrm{16}−\mathrm{3t}} \\ $$$$\Rightarrow\:\:\left(\mathrm{t}+\mathrm{8}\right)^{\mathrm{2}} =\mathrm{64}−\mathrm{12t} \\ $$$$\Rightarrow\:\:\mathrm{t}^{\mathrm{2}} +\mathrm{28t}=\mathrm{0} \\ $$$$\mathrm{or}\:\:\:\:\:\mathrm{t}=\mathrm{0},\:−\mathrm{28}\:;\:\:\mathrm{but}\:\mathrm{t}\geqslant\mathrm{0}\:,\:\:\mathrm{so} \\ $$$$\:\:\:\:\:\mathrm{t}=\mathrm{0}\:\:,\:\:\mathrm{x}=\mathrm{2}\:. \\ $$$$\mathrm{At}\:\mathrm{x}=\mathrm{2}\:,\:\:\mathrm{17}+\mathrm{8x}−\mathrm{2x}^{\mathrm{2}} \:>\:\mathrm{0} \\ $$$$\mathrm{and}\:\:\mathrm{4}+\mathrm{12x}−\mathrm{3x}^{\mathrm{2}} \:>\:\mathrm{0} \\ $$$$\mathrm{so}\:\mathrm{no}\:\mathrm{objection}\:\mathrm{to}\:\:\mathrm{x}=\mathrm{2}\:. \\ $$
Commented by aknabob last updated on 13/Aug/17

$${pls}\:{its}\:{not}\:{clear} \\ $$
Commented by Tinkutara last updated on 13/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
