Menu Close

Find-the-remainder-when-1-1-2-2-3-3-100-100-is-divided-by-101-

Tinku Tara 0 Comments
Pin




Question Number 119097 by ZiYangLee last updated on 22/Oct/20
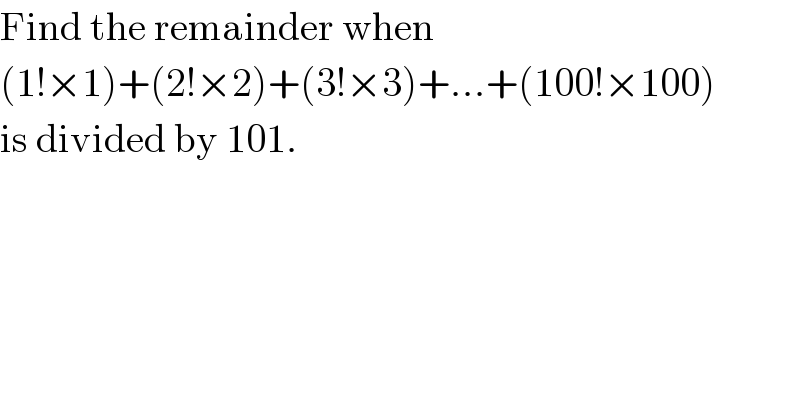
Find the remainder when (1!×1)+(2!×2)+(3!×3)+...+(100!×100) is divided by 101.
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\: \\ $$$$\left(\mathrm{1}!×\mathrm{1}\right)+\left(\mathrm{2}!×\mathrm{2}\right)+\left(\mathrm{3}!×\mathrm{3}\right)+…+\left(\mathrm{100}!×\mathrm{100}\right) \\ $$$$\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{101}. \\ $$
Answered by mindispower last updated on 22/Oct/20
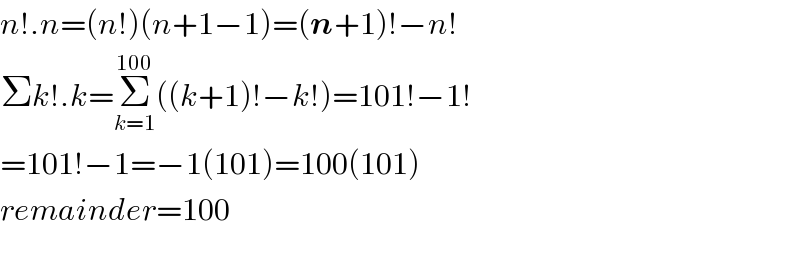
n!.n=(n!)(n+1−1)=(n+1)!−n! Σk!.k=Σ_(k=1) ^(100) ((k+1)!−k!)=101!−1! =101!−1=−1(101)=100(101) remainder=100
$${n}!.{n}=\left({n}!\right)\left({n}+\mathrm{1}−\mathrm{1}\right)=\left(\boldsymbol{{n}}+\mathrm{1}\right)!−{n}! \\ $$$$\Sigma{k}!.{k}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\left(\left({k}+\mathrm{1}\right)!−{k}!\right)=\mathrm{101}!−\mathrm{1}! \\ $$$$=\mathrm{101}!−\mathrm{1}=−\mathrm{1}\left(\mathrm{101}\right)=\mathrm{100}\left(\mathrm{101}\right) \\ $$$${remainder}=\mathrm{100} \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 22/Oct/20
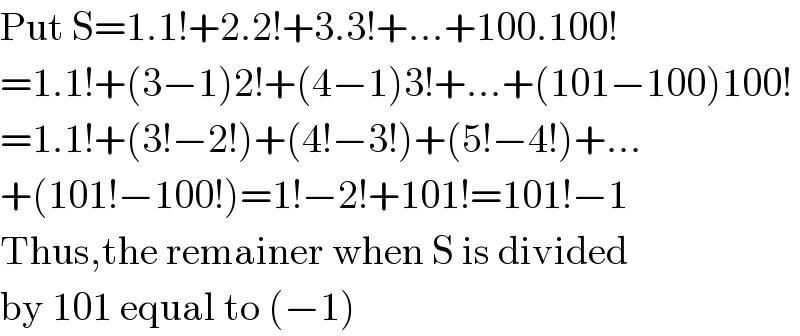
Put S=1.1!+2.2!+3.3!+...+100.100! =1.1!+(3−1)2!+(4−1)3!+...+(101−100)100! =1.1!+(3!−2!)+(4!−3!)+(5!−4!)+... +(101!−100!)=1!−2!+101!=101!−1 Thus,the remainer when S is divided by 101 equal to (−1)
$$\mathrm{Put}\:\mathrm{S}=\mathrm{1}.\mathrm{1}!+\mathrm{2}.\mathrm{2}!+\mathrm{3}.\mathrm{3}!+…+\mathrm{100}.\mathrm{100}! \\ $$$$=\mathrm{1}.\mathrm{1}!+\left(\mathrm{3}−\mathrm{1}\right)\mathrm{2}!+\left(\mathrm{4}−\mathrm{1}\right)\mathrm{3}!+…+\left(\mathrm{101}−\mathrm{100}\right)\mathrm{100}! \\ $$$$=\mathrm{1}.\mathrm{1}!+\left(\mathrm{3}!−\mathrm{2}!\right)+\left(\mathrm{4}!−\mathrm{3}!\right)+\left(\mathrm{5}!−\mathrm{4}!\right)+… \\ $$$$+\left(\mathrm{101}!−\mathrm{100}!\right)=\mathrm{1}!−\mathrm{2}!+\mathrm{101}!=\mathrm{101}!−\mathrm{1} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{remainer}\:\mathrm{when}\:\mathrm{S}\:\mathrm{is}\:\mathrm{divided} \\ $$$$\mathrm{by}\:\mathrm{101}\:\mathrm{equal}\:\mathrm{to}\:\left(−\mathrm{1}\right) \\ $$
Commented by PRITHWISH SEN 2 last updated on 22/Oct/20
−1 can′t be a remainder it will be written as 100−101= 100 as remainder
$$−\mathrm{1}\:\mathrm{can}'\mathrm{t}\:\mathrm{be}\:\mathrm{a}\:\mathrm{remainder}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as} \\ $$$$\mathrm{100}−\mathrm{101}=\:\mathrm{100}\:\mathrm{as}\:\mathrm{remainder} \\ $$
Commented by 1549442205PVT last updated on 25/Oct/20
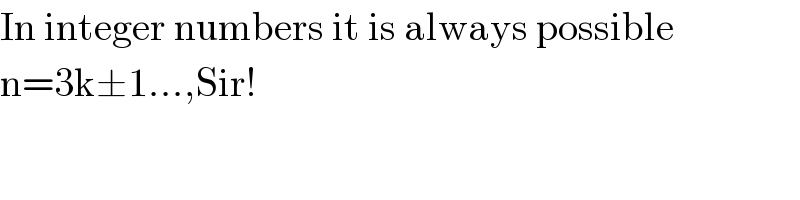
In integer numbers it is always possible n=3k±1...,Sir!
$$\mathrm{In}\:\mathrm{integer}\:\mathrm{numbers}\:\mathrm{it}\:\mathrm{is}\:\mathrm{always}\:\mathrm{possible} \\ $$$$\mathrm{n}=\mathrm{3k}\pm\mathrm{1}…,\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *