Find-the-remainder-when-55-99-is-divided-by-14-

Question Number 14715 by tawa tawa last updated on 03/Jun/17

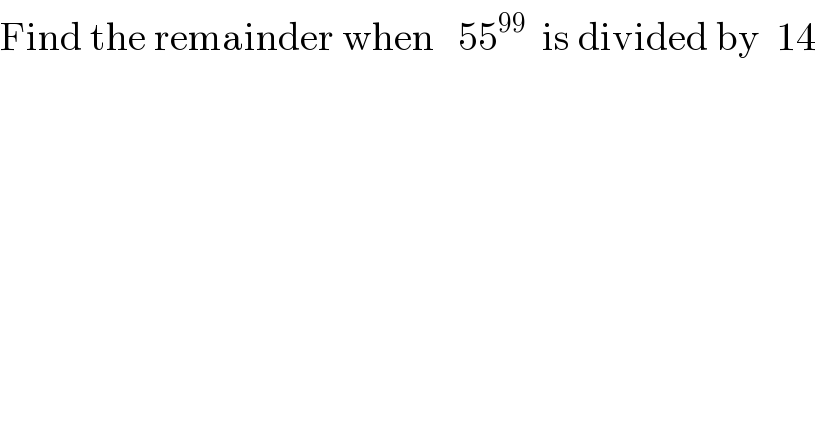
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\:\:\:\mathrm{55}^{\mathrm{99}} \:\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\:\mathrm{14} \\ $$

Commented by prakash jain last updated on 04/Jun/17

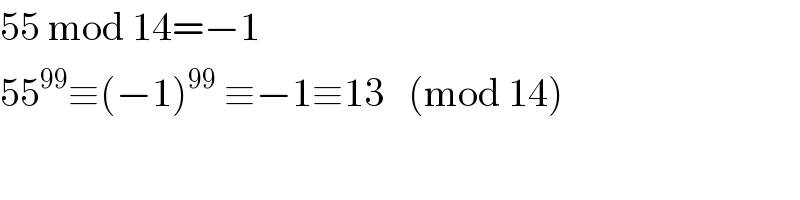
55 mod 14=−1 55^(99) ≡(−1)^(99) ≡−1≡13 (mod 14)

$$\mathrm{55}\:\mathrm{mod}\:\mathrm{14}=−\mathrm{1} \\ $$$$\mathrm{55}^{\mathrm{99}} \equiv\left(−\mathrm{1}\right)^{\mathrm{99}} \:\equiv−\mathrm{1}\equiv\mathrm{13}\:\:\:\left(\mathrm{mod}\:\mathrm{14}\right) \\ $$

Commented by Tinkutara last updated on 04/Jun/17

$$\mathrm{Very}\:\mathrm{simple}\:\mathrm{and}\:\mathrm{short}\:\mathrm{method}!\:\mathrm{Thanks}! \\ $$

Answered by mrW1 last updated on 04/Jun/17

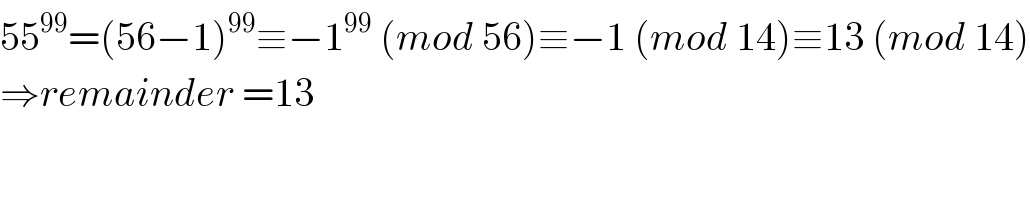
55^(99) =(56−1)^(99) ≡−1^(99) (mod 56)≡−1 (mod 14)≡13 (mod 14) ⇒remainder =13

$$\mathrm{55}^{\mathrm{99}} =\left(\mathrm{56}−\mathrm{1}\right)^{\mathrm{99}} \equiv−\mathrm{1}^{\mathrm{99}} \:\left({mod}\:\mathrm{56}\right)\equiv−\mathrm{1}\:\left({mod}\:\mathrm{14}\right)\equiv\mathrm{13}\:\left({mod}\:\mathrm{14}\right) \\ $$$$\Rightarrow{remainder}\:=\mathrm{13} \\ $$

Commented by RasheedSoomro last updated on 04/Jun/17

$$\mathrm{Thanks}\:\mathcal{S}\mathrm{ir}! \\ $$

Commented by RasheedSoomro last updated on 04/Jun/17

Pl write in some detail and with reasons.

$$\mathrm{Pl}\:\mathrm{write}\:\mathrm{in}\:\mathrm{some}\:\mathrm{detail}\:\mathrm{and}\:\mathrm{with}\:\mathrm{reasons}. \\ $$

Commented by Tinkutara last updated on 04/Jun/17

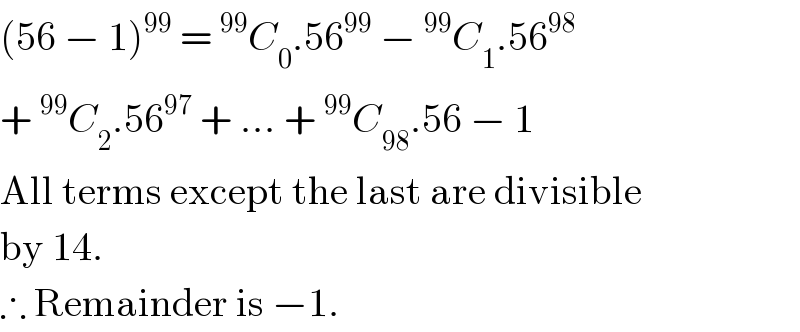
(56 − 1)^(99) =^(99) C_0 .56^(99) −^(99) C_1 .56^(98) +^(99) C_2 .56^(97) + ... +^(99) C_(98) .56 − 1 All terms except the last are divisible by 14. ∴ Remainder is −1.

$$\left(\mathrm{56}\:−\:\mathrm{1}\right)^{\mathrm{99}} \:=\:^{\mathrm{99}} {C}_{\mathrm{0}} .\mathrm{56}^{\mathrm{99}} \:−\:^{\mathrm{99}} {C}_{\mathrm{1}} .\mathrm{56}^{\mathrm{98}} \\ $$$$+\:^{\mathrm{99}} {C}_{\mathrm{2}} .\mathrm{56}^{\mathrm{97}} \:+\:…\:+\:^{\mathrm{99}} {C}_{\mathrm{98}} .\mathrm{56}\:−\:\mathrm{1} \\ $$$$\mathrm{All}\:\mathrm{terms}\:\mathrm{except}\:\mathrm{the}\:\mathrm{last}\:\mathrm{are}\:\mathrm{divisible} \\ $$$$\mathrm{by}\:\mathrm{14}. \\ $$$$\therefore\:\mathrm{Remainder}\:\mathrm{is}\:−\mathrm{1}. \\ $$

Answered by RasheedSoomro last updated on 04/Jun/17

φ(14)=14(1−(1/2))(1−(1/7)) [ ∵ 14=2×7] =1×6=6 Because (55,14)=1 So 55^6 ≡1(mod 14) ( 55^6 )^(16) ≡(1)^(16) (mod 14 55^(96) ≡1(mod 14)........(i) 5^3 ≡13(mod 14)........................(ii) (i)×(ii): 5^(99) ≡13(mod 14)

$$\phi\left(\mathrm{14}\right)=\mathrm{14}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{7}}\right)\:\:\:\left[\:\because\:\:\mathrm{14}=\mathrm{2}×\mathrm{7}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}×\mathrm{6}=\mathrm{6} \\ $$$$ \\ $$$$\mathrm{Because}\:\left(\mathrm{55},\mathrm{14}\right)=\mathrm{1} \\ $$$$\mathrm{So}\:\:\:\:\mathrm{55}^{\mathrm{6}} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{14}\right) \\ $$$$\:\:\:\:\:\:\:\:\left(\:\mathrm{55}^{\mathrm{6}} \right)^{\mathrm{16}} \equiv\left(\mathrm{1}\right)^{\mathrm{16}} \left(\mathrm{mod}\:\mathrm{14}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{55}^{\mathrm{96}} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{14}\right)……..\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{5}^{\mathrm{3}} \equiv\mathrm{13}\left(\mathrm{mod}\:\mathrm{14}\right)……………………\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)×\left(\mathrm{ii}\right): \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{5}^{\mathrm{99}} \equiv\mathrm{13}\left(\mathrm{mod}\:\mathrm{14}\right) \\ $$

Commented by tawa tawa last updated on 04/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by RasheedSoomro last updated on 04/Jun/17

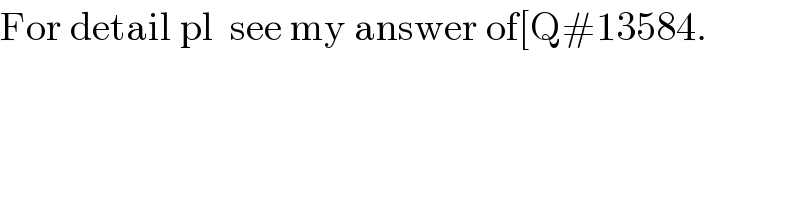
$$\mathrm{For}\:\mathrm{detail}\:\mathrm{pl}\:\:\mathrm{see}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{of}\left[\mathrm{Q}#\mathrm{13584}.\right. \\ $$

Facebook Tweet Pin

Find-the-remainder-when-55-99-is-divided-by-14-

Leave a Reply Cancel reply