Question Number 113928 by ZiYangLee last updated on 16/Sep/20
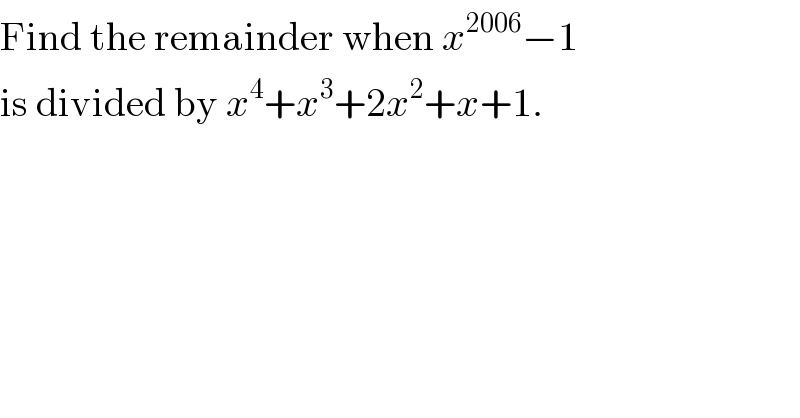
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\:{x}^{\mathrm{2006}} −\mathrm{1}\: \\ $$$$\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}. \\ $$
Answered by MJS_new last updated on 16/Sep/20
![x^4 +x^3 +2x^2 +x+1=(x^2 +1)(x^2 +x+1) the remaining fractions of ((x^(2n) −1)/((x^2 +1)(x^2 +x+1))) are 0 for n=6k ((x^2 −1)/((x^2 +1)(x^2 +x+1))) for n=6k+1 [2006=2(6×167+1)] −((x+2)/(x^2 +x+1)) for n=6k+2 ((2x)/(x^2 +1)) for n=6k+3 −((2x+1)/(x^2 +x+1)) for n=6k+4 ((x^3 +x−2)/((x^2 +1)(x^2 +x+1))) for n=6k+5](https://www.tinkutara.com/question/Q113943.png)
$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{1}=\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$$$\mathrm{the}\:\mathrm{remaining}\:\mathrm{fractions}\:\mathrm{of} \\ $$$$\frac{{x}^{\mathrm{2}{n}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)} \\ $$$$\mathrm{are} \\ $$$$\mathrm{0}\:\mathrm{for}\:{n}=\mathrm{6}{k} \\ $$$$\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{1}\:\left[\mathrm{2006}=\mathrm{2}\left(\mathrm{6}×\mathrm{167}+\mathrm{1}\right)\right] \\ $$$$−\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{2} \\ $$$$\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{3} \\ $$$$−\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{4} \\ $$$$\frac{{x}^{\mathrm{3}} +{x}−\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}\:\mathrm{for}\:{n}=\mathrm{6}{k}+\mathrm{5} \\ $$
Commented by 1549442205PVT last updated on 16/Sep/20
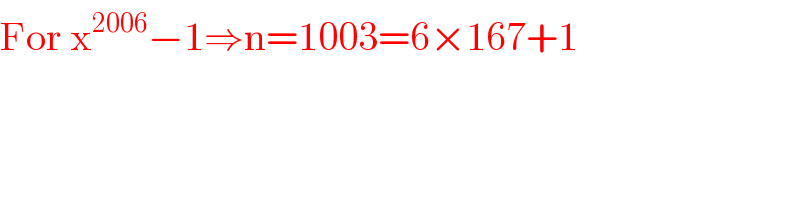
$$\mathrm{For}\:\mathrm{x}^{\mathrm{2006}} −\mathrm{1}\Rightarrow\mathrm{n}=\mathrm{1003}=\mathrm{6}×\mathrm{167}+\mathrm{1} \\ $$
Commented by MJS_new last updated on 16/Sep/20
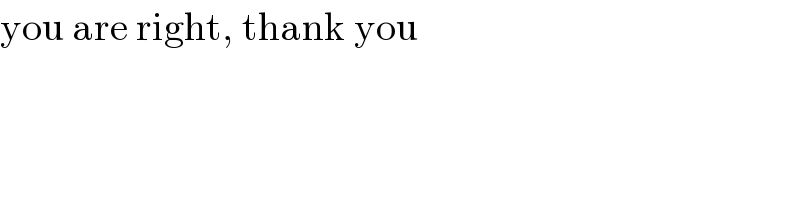
$$\mathrm{you}\:\mathrm{are}\:\mathrm{right},\:\mathrm{thank}\:\mathrm{you} \\ $$
