Question Number 31194 by U Htay KyawMyint last updated on 03/Mar/18
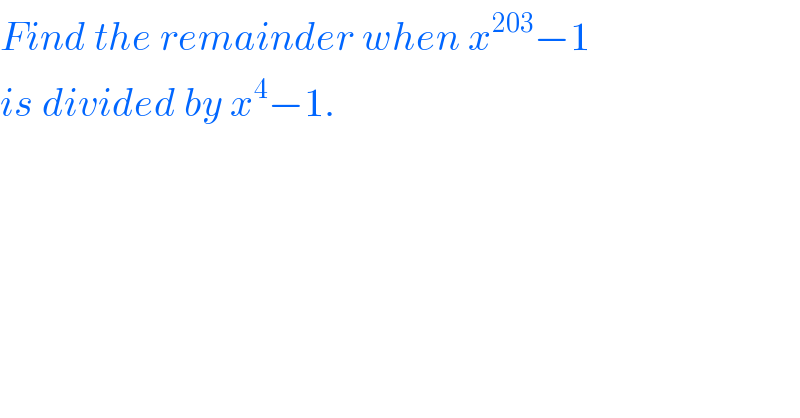
$${Find}\:{the}\:{remainder}\:{when}\:{x}^{\mathrm{203}} −\mathrm{1} \\ $$$${is}\:{divided}\:{by}\:{x}^{\mathrm{4}} −\mathrm{1}. \\ $$
Commented by 6123 last updated on 04/Mar/18
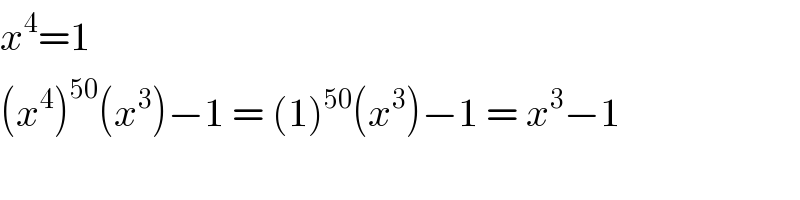
$${x}^{\mathrm{4}} =\mathrm{1} \\ $$$$\left({x}^{\mathrm{4}} \right)^{\mathrm{50}} \left({x}^{\mathrm{3}} \right)−\mathrm{1}\:=\:\left(\mathrm{1}\right)^{\mathrm{50}} \left({x}^{\mathrm{3}} \right)−\mathrm{1}\:=\:{x}^{\mathrm{3}} −\mathrm{1} \\ $$
Answered by math solver last updated on 03/Mar/18

$${x}^{\mathrm{3}} −\mathrm{1}\:. \\ $$
Commented by MJS last updated on 04/Mar/18
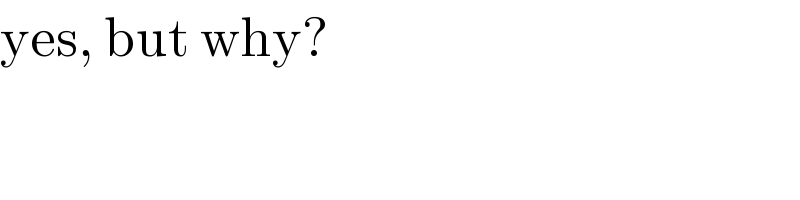
$$\mathrm{yes},\:\mathrm{but}\:\mathrm{why}? \\ $$
Answered by mrW2 last updated on 04/Mar/18
![x^(203) −1 =x^3 ×x^(200) −1 =x^3 ×(x^4 )^(50) −1 =x^3 ×[(x^4 −1)+1]^(50) −1 =x^3 ×[(......)+1]−1 with (......)=terms with factor(x^4 −1) =x^3 (......)+(x^3 −1) ⇒when 2^(203) −1 is divided by x^4 −1, the remainder is x^3 −1.](https://www.tinkutara.com/question/Q31231.png)
$${x}^{\mathrm{203}} −\mathrm{1} \\ $$$$={x}^{\mathrm{3}} ×{x}^{\mathrm{200}} −\mathrm{1} \\ $$$$={x}^{\mathrm{3}} ×\left({x}^{\mathrm{4}} \right)^{\mathrm{50}} −\mathrm{1} \\ $$$$={x}^{\mathrm{3}} ×\left[\left({x}^{\mathrm{4}} −\mathrm{1}\right)+\mathrm{1}\right]^{\mathrm{50}} −\mathrm{1} \\ $$$$={x}^{\mathrm{3}} ×\left[\left(……\right)+\mathrm{1}\right]−\mathrm{1} \\ $$$${with}\:\left(……\right)={terms}\:{with}\:{factor}\left({x}^{\mathrm{4}} −\mathrm{1}\right) \\ $$$$={x}^{\mathrm{3}} \left(……\right)+\left({x}^{\mathrm{3}} −\mathrm{1}\right) \\ $$$$\Rightarrow{when}\:\mathrm{2}^{\mathrm{203}} −\mathrm{1}\:{is}\:{divided}\:{by}\:{x}^{\mathrm{4}} −\mathrm{1}, \\ $$$${the}\:{remainder}\:{is}\:{x}^{\mathrm{3}} −\mathrm{1}. \\ $$
Commented by MJS last updated on 04/Mar/18

$$\mathrm{thank}\:\mathrm{you} \\ $$
