Menu Close

find-the-residue-of-f-z-sin-z-cos-z-3-1-

Tinku Tara 0 Comments
Pin




Question Number 148174 by tabata last updated on 25/Jul/21
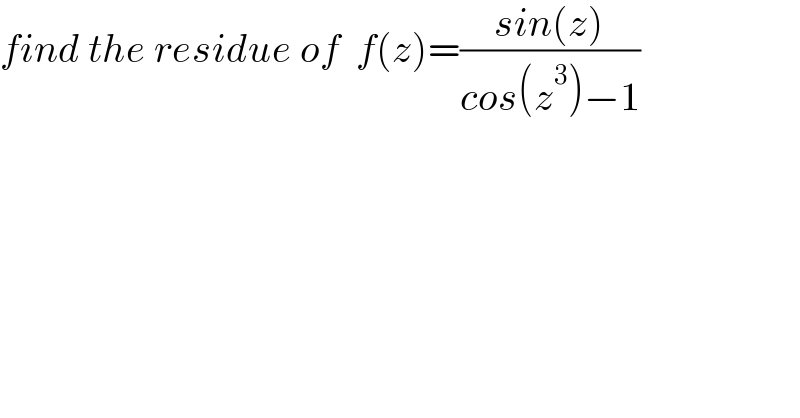
find the residue of f(z)=((sin(z))/(cos(z^3 )−1))
$${find}\:{the}\:{residue}\:{of}\:\:{f}\left({z}\right)=\frac{{sin}\left({z}\right)}{{cos}\left({z}^{\mathrm{3}} \right)−\mathrm{1}} \\ $$
Answered by mathmax by abdo last updated on 25/Jul/21
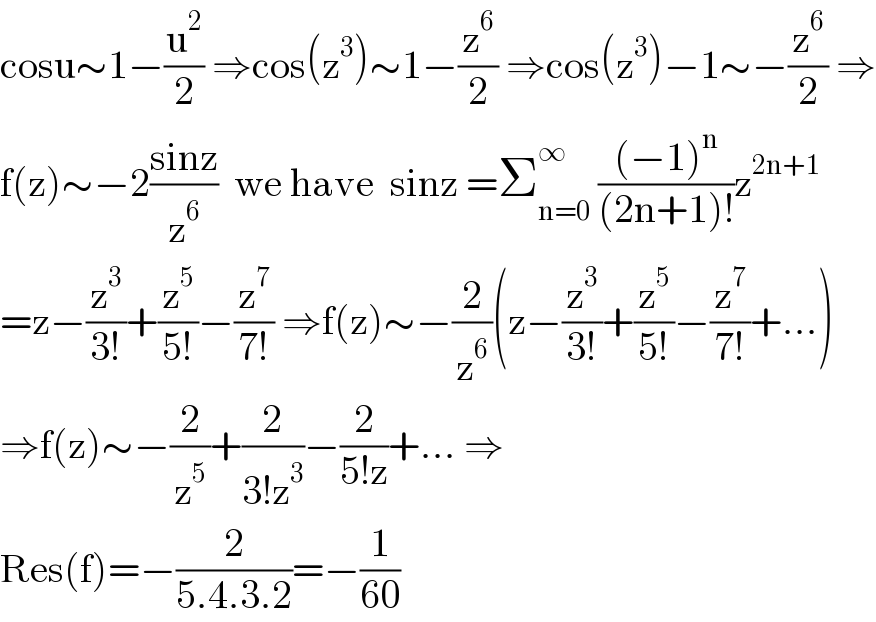
cosu∼1−(u^2 /2) ⇒cos(z^3 )∼1−(z^6 /2) ⇒cos(z^3 )−1∼−(z^6 /2) ⇒ f(z)∼−2((sinz)/z^6 ) we have sinz =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!))z^(2n+1) =z−(z^3 /(3!))+(z^5 /(5!))−(z^7 /(7!)) ⇒f(z)∼−(2/z^6 )(z−(z^3 /(3!))+(z^5 /(5!))−(z^7 /(7!))+...) ⇒f(z)∼−(2/z^5 )+(2/(3!z^3 ))−(2/(5!z))+... ⇒ Res(f)=−(2/(5.4.3.2))=−(1/(60))
$$\mathrm{cosu}\sim\mathrm{1}−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{cos}\left(\mathrm{z}^{\mathrm{3}} \right)\sim\mathrm{1}−\frac{\mathrm{z}^{\mathrm{6}} }{\mathrm{2}}\:\Rightarrow\mathrm{cos}\left(\mathrm{z}^{\mathrm{3}} \right)−\mathrm{1}\sim−\frac{\mathrm{z}^{\mathrm{6}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)\sim−\mathrm{2}\frac{\mathrm{sinz}}{\mathrm{z}^{\mathrm{6}} }\:\:\mathrm{we}\:\mathrm{have}\:\:\mathrm{sinz}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\mathrm{z}^{\mathrm{2n}+\mathrm{1}} \\ $$$$=\mathrm{z}−\frac{\mathrm{z}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{z}^{\mathrm{5}} }{\mathrm{5}!}−\frac{\mathrm{z}^{\mathrm{7}} }{\mathrm{7}!}\:\Rightarrow\mathrm{f}\left(\mathrm{z}\right)\sim−\frac{\mathrm{2}}{\mathrm{z}^{\mathrm{6}} }\left(\mathrm{z}−\frac{\mathrm{z}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{z}^{\mathrm{5}} }{\mathrm{5}!}−\frac{\mathrm{z}^{\mathrm{7}} }{\mathrm{7}!}+…\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{z}\right)\sim−\frac{\mathrm{2}}{\mathrm{z}^{\mathrm{5}} }+\frac{\mathrm{2}}{\mathrm{3}!\mathrm{z}^{\mathrm{3}} }−\frac{\mathrm{2}}{\mathrm{5}!\mathrm{z}}+…\:\Rightarrow \\ $$$$\mathrm{Res}\left(\mathrm{f}\right)=−\frac{\mathrm{2}}{\mathrm{5}.\mathrm{4}.\mathrm{3}.\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{60}} \\ $$
Answered by Olaf_Thorendsen last updated on 25/Jul/21
f(z) = ((sinz)/(cos(z^3 )−1)) f(z) = ((sinz)/((1−(z^6 /2)+(z^(12) /(24))−(z^(18) /(720))...)−1)) f(z) = ((sinz)/(−(z^6 /2)+(z^(12) /(24))−(z^(18) /(720))+...)) f(z) = −(2/z^6 ).((sinz)/(1−((z^6 /(12))−(z^(12) /(360))+...))) f(z) = −((2sinz)/z^6 )[1+((z^6 /(12))−(z^(12) /(360))+...)+((z^6 /(12))−(z^(12) /(360))+...)^2 +...] f(z) = −((2(z−(z^3 /6)+(z^5 /(120))...))/z^6 )[1+((z^6 /(12))−(z^(12) /(360))+...)+((z^6 /(12))−(z^(12) /(360))+...)^2 +...] f(z) = −(2/z^5 )+(1/(3z^3 ))−(1/(60z))−((421)/(2520)) z+.. The term in z^(−1) is −(1/(60)) ⇒The residue is −(1/(60)).
$${f}\left({z}\right)\:=\:\frac{\mathrm{sin}{z}}{\mathrm{cos}\left({z}^{\mathrm{3}} \right)−\mathrm{1}} \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{sin}{z}}{\left(\mathrm{1}−\frac{{z}^{\mathrm{6}} }{\mathrm{2}}+\frac{{z}^{\mathrm{12}} }{\mathrm{24}}−\frac{{z}^{\mathrm{18}} }{\mathrm{720}}…\right)−\mathrm{1}} \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{sin}{z}}{−\frac{{z}^{\mathrm{6}} }{\mathrm{2}}+\frac{{z}^{\mathrm{12}} }{\mathrm{24}}−\frac{{z}^{\mathrm{18}} }{\mathrm{720}}+…} \\ $$$${f}\left({z}\right)\:=\:−\frac{\mathrm{2}}{{z}^{\mathrm{6}} }.\frac{\mathrm{sin}{z}}{\mathrm{1}−\left(\frac{{z}^{\mathrm{6}} }{\mathrm{12}}−\frac{{z}^{\mathrm{12}} }{\mathrm{360}}+…\right)} \\ $$$${f}\left({z}\right)\:=\:−\frac{\mathrm{2sin}{z}}{{z}^{\mathrm{6}} }\left[\mathrm{1}+\left(\frac{{z}^{\mathrm{6}} }{\mathrm{12}}−\frac{{z}^{\mathrm{12}} }{\mathrm{360}}+…\right)+\left(\frac{{z}^{\mathrm{6}} }{\mathrm{12}}−\frac{{z}^{\mathrm{12}} }{\mathrm{360}}+…\right)^{\mathrm{2}} +…\right] \\ $$$${f}\left({z}\right)\:=\:−\frac{\mathrm{2}\left({z}−\frac{{z}^{\mathrm{3}} }{\mathrm{6}}+\frac{{z}^{\mathrm{5}} }{\mathrm{120}}…\right)}{{z}^{\mathrm{6}} }\left[\mathrm{1}+\left(\frac{{z}^{\mathrm{6}} }{\mathrm{12}}−\frac{{z}^{\mathrm{12}} }{\mathrm{360}}+…\right)+\left(\frac{{z}^{\mathrm{6}} }{\mathrm{12}}−\frac{{z}^{\mathrm{12}} }{\mathrm{360}}+…\right)^{\mathrm{2}} +…\right] \\ $$$${f}\left({z}\right)\:=\:−\frac{\mathrm{2}}{{z}^{\mathrm{5}} }+\frac{\mathrm{1}}{\mathrm{3}{z}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{60}{z}}−\frac{\mathrm{421}}{\mathrm{2520}}\:{z}+.. \\ $$$$\mathrm{The}\:\mathrm{term}\:\mathrm{in}\:{z}^{−\mathrm{1}} \:\mathrm{is}\:−\frac{\mathrm{1}}{\mathrm{60}} \\ $$$$\Rightarrow\mathrm{The}\:\mathrm{residue}\:\mathrm{is}\:−\frac{\mathrm{1}}{\mathrm{60}}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *