Question Number 62585 by Jmasanja last updated on 23/Jun/19

$${find}\:{the}\:{resultant}\:{force}\:{of}\:{a}\:{system} \\ $$$${of}\:{three}\:{forces}\:\overset{−} {{O}}\overset{\rightarrow} {{P}}\:=\mathrm{9}{N},\overset{−} {{O}}\overset{\rightarrow} {{R}}\:=\mathrm{10}{N}\:{and}\:\overset{−} {{O}}\overset{\rightarrow} {{Q}}\:\mathrm{10}{N}\: \\ $$$${acting}\:{at}\:{point}\:{O}\:{where}\:{angle}\:{POR}\:{is} \\ $$$$\mathrm{135}°,{angle}\:{POQ}\:{is}\:\mathrm{135}°\:\:{and}\:{QOR}\:{is}\: \\ $$$$\mathrm{90}° \\ $$
Answered by MJS last updated on 23/Jun/19
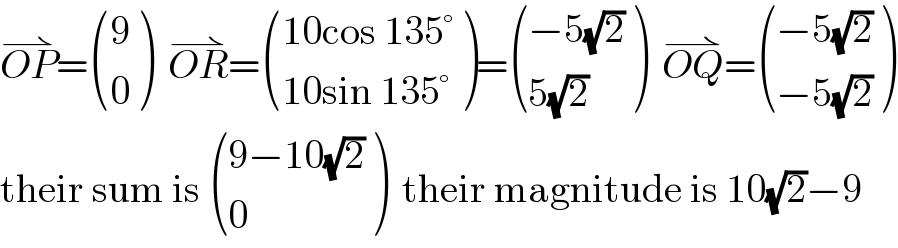
$$\overset{\rightharpoonup} {{OP}}=\begin{pmatrix}{\mathrm{9}}\\{\mathrm{0}}\end{pmatrix}\:\:\overset{\rightharpoonup} {{OR}}=\begin{pmatrix}{\mathrm{10cos}\:\mathrm{135}°}\\{\mathrm{10sin}\:\mathrm{135}°}\end{pmatrix}=\begin{pmatrix}{−\mathrm{5}\sqrt{\mathrm{2}}}\\{\mathrm{5}\sqrt{\mathrm{2}}}\end{pmatrix}\:\:\overset{\rightharpoonup} {{OQ}}=\begin{pmatrix}{−\mathrm{5}\sqrt{\mathrm{2}}}\\{−\mathrm{5}\sqrt{\mathrm{2}}}\end{pmatrix} \\ $$$$\mathrm{their}\:\mathrm{sum}\:\mathrm{is}\:\begin{pmatrix}{\mathrm{9}−\mathrm{10}\sqrt{\mathrm{2}}}\\{\mathrm{0}}\end{pmatrix}\:\:\mathrm{their}\:\mathrm{magnitude}\:\mathrm{is}\:\mathrm{10}\sqrt{\mathrm{2}}−\mathrm{9} \\ $$
