Question Number 172025 by Mikenice last updated on 23/Jun/22
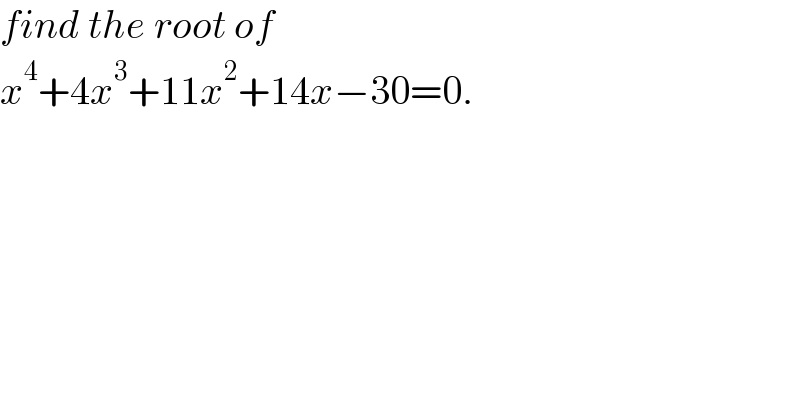
$${find}\:{the}\:{root}\:{of}\: \\ $$$${x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{11}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{30}=\mathrm{0}. \\ $$
Answered by thfchristopher last updated on 23/Jun/22

$${x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{11}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{30}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} +\mathrm{16}{x}+\mathrm{30}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{1}\right)\left({x}+\mathrm{3}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{10}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{1}\right)\left({x}+\mathrm{3}\right)\left({x}+\mathrm{1}+\mathrm{3}{i}\right)\left({x}+\mathrm{1}−\mathrm{3}{i}\right)=\mathrm{0} \\ $$$$\therefore\:{x}=\mathrm{1},\:−\mathrm{3},\:−\mathrm{1}\pm\mathrm{3}{i} \\ $$
