Question Number 78568 by TawaTawa last updated on 18/Jan/20
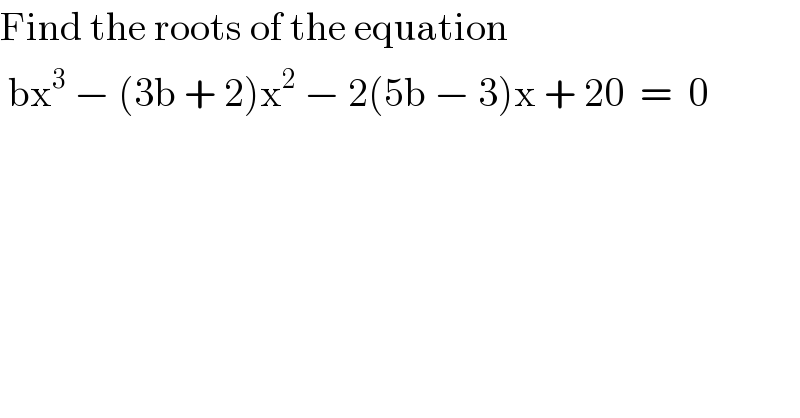
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\:\mathrm{bx}^{\mathrm{3}} \:−\:\left(\mathrm{3b}\:+\:\mathrm{2}\right)\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{2}\left(\mathrm{5b}\:−\:\mathrm{3}\right)\mathrm{x}\:+\:\mathrm{20}\:\:=\:\:\mathrm{0} \\ $$
Answered by key of knowledge last updated on 18/Jan/20
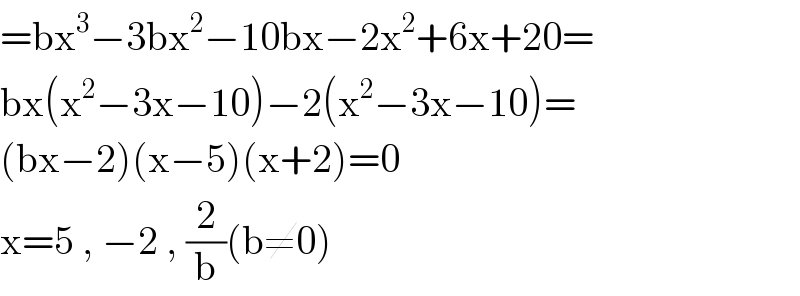
$$=\mathrm{bx}^{\mathrm{3}} −\mathrm{3bx}^{\mathrm{2}} −\mathrm{10bx}−\mathrm{2x}^{\mathrm{2}} +\mathrm{6x}+\mathrm{20}= \\ $$$$\mathrm{bx}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{10}\right)−\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}−\mathrm{10}\right)= \\ $$$$\left(\mathrm{bx}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{5}\right)\left(\mathrm{x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{x}=\mathrm{5}\:,\:−\mathrm{2}\:,\:\frac{\mathrm{2}}{\mathrm{b}}\left(\mathrm{b}\neq\mathrm{0}\right) \\ $$
Commented by TawaTawa last updated on 18/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
