Find-the-semi-interquartile-range-of-of-the-following-numbers-15-10-9-15-15-8-10-11-8-12-11-14-9-and-15-

Question Number 95789 by Don08q last updated on 27/May/20

$$\:\mathrm{Find}\:\mathrm{the}\:\mathrm{semi}−\mathrm{interquartile}\:\mathrm{range}\:\mathrm{of}\: \\ $$$$\:\mathrm{of}\:\mathrm{the}\:\mathrm{following}\:\mathrm{numbers}: \\ $$$$\:\mathrm{15},\:\mathrm{10},\:\mathrm{9},\:\mathrm{15},\:\mathrm{15},\:\mathrm{8},\:\mathrm{10},\:\mathrm{11},\:\mathrm{8},\:\mathrm{12},\:\mathrm{11},\:\mathrm{14}, \\ $$$$\:\mathrm{9}\:\mathrm{and}\:\mathrm{15} \\ $$

Commented by Don08q last updated on 27/May/20

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}. \\ $$

Answered by prakash jain last updated on 27/May/20

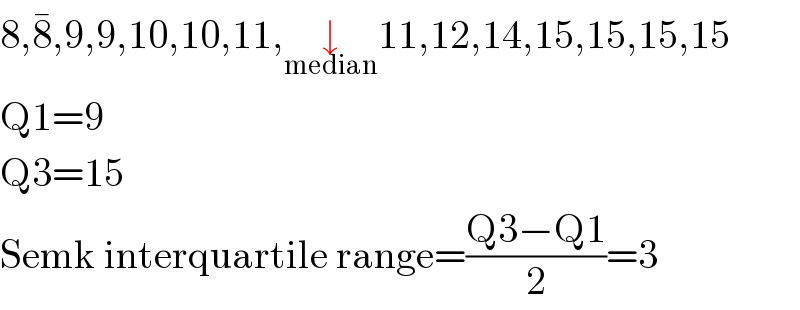
$$\mathrm{8},\bar {\mathrm{8}},\mathrm{9},\mathrm{9},\mathrm{10},\mathrm{10},\mathrm{11},\underset{\mathrm{median}} {\downarrow}\mathrm{11},\mathrm{12},\mathrm{14},\mathrm{15},\mathrm{15},\mathrm{15},\mathrm{15} \\ $$$$\mathrm{Q1}=\mathrm{9} \\ $$$$\mathrm{Q3}=\mathrm{15} \\ $$$$\mathrm{Semk}\:\mathrm{interquartile}\:\mathrm{range}=\frac{\mathrm{Q3}−\mathrm{Q1}}{\mathrm{2}}=\mathrm{3} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com