Question Number 49961 by maxmathsup by imad last updated on 12/Dec/18

$${find}\:{the}\:{sequence}\:\left({a}_{{n}} \right)\:{wich}\:{verify}\: \\ $$$$\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:{x}^{{n}} \right)\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−{x}\right)^{{n}} }{{n}+\mathrm{1}}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:{a}_{{n}} {x}^{{n}} \:\:{also}\:{find}\:{the}\:{radius}\:{of}\:{this}\:{serie}. \\ $$
Commented by Abdo msup. last updated on 13/Dec/18
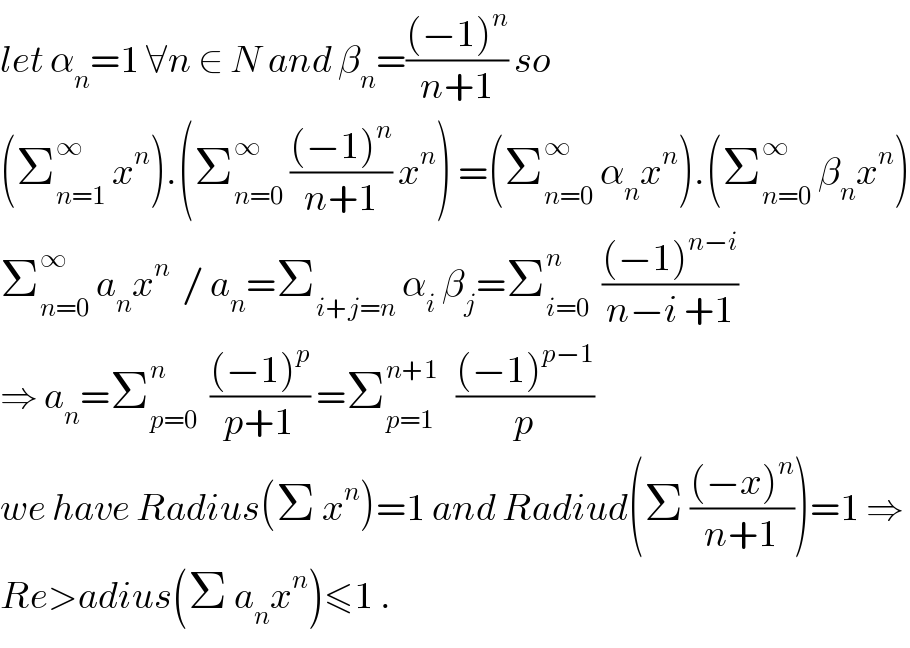
$${let}\:\alpha_{{n}} =\mathrm{1}\:\forall{n}\:\in\:{N}\:{and}\:\beta_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:{so} \\ $$$$\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:{x}^{{n}} \right).\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:{x}^{{n}} \right)\:=\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\alpha_{{n}} {x}^{{n}} \right).\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\beta_{{n}} {x}^{{n}} \right) \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:{a}_{{n}} {x}^{{n}} \:\:/\:{a}_{{n}} =\sum_{{i}+{j}={n}} \:\alpha_{{i}} \:\beta_{{j}} =\sum_{{i}=\mathrm{0}} ^{{n}} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−{i}} }{{n}−{i}\:+\mathrm{1}} \\ $$$$\Rightarrow\:{a}_{{n}} =\sum_{{p}=\mathrm{0}} ^{{n}} \:\:\frac{\left(−\mathrm{1}\right)^{{p}} }{{p}+\mathrm{1}}\:=\sum_{{p}=\mathrm{1}} ^{{n}+\mathrm{1}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{p}−\mathrm{1}} }{{p}} \\ $$$${we}\:{have}\:{Radius}\left(\Sigma\:{x}^{{n}} \right)=\mathrm{1}\:{and}\:{Radiud}\left(\Sigma\:\frac{\left(−{x}\right)^{{n}} }{{n}+\mathrm{1}}\right)=\mathrm{1}\:\Rightarrow \\ $$$${Re}>{adius}\left(\Sigma\:{a}_{{n}} {x}^{{n}} \right)\leqslant\mathrm{1}\:. \\ $$
