find-the-sequence-v-n-wich-verify-v-n-2-v-n-v-n-1-

Question Number 32996 by abdo imad last updated on 09/Apr/18

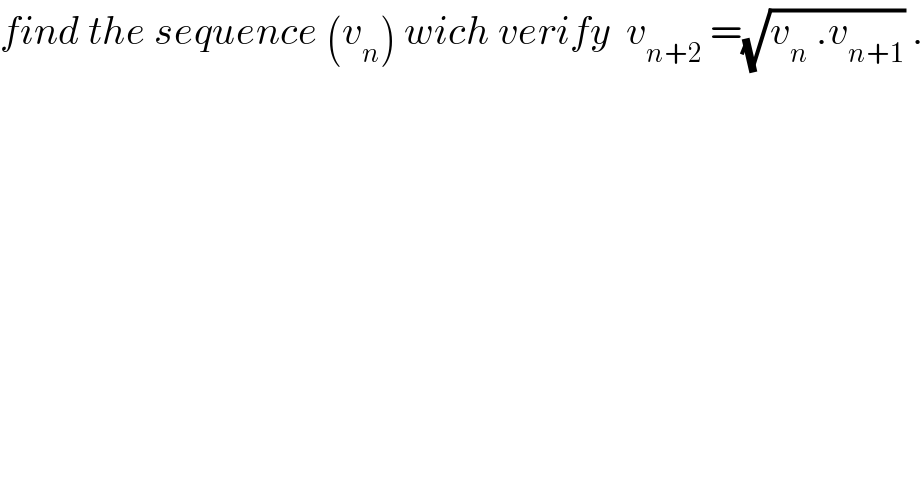
f i n d t h e s e q u e n c e (v_{n}) w i c h v e r i f y v_{n + 2} = \sqrt{v_{n} . v_{n + 1}} .

Commented by prof Abdo imad last updated on 11/Apr/18

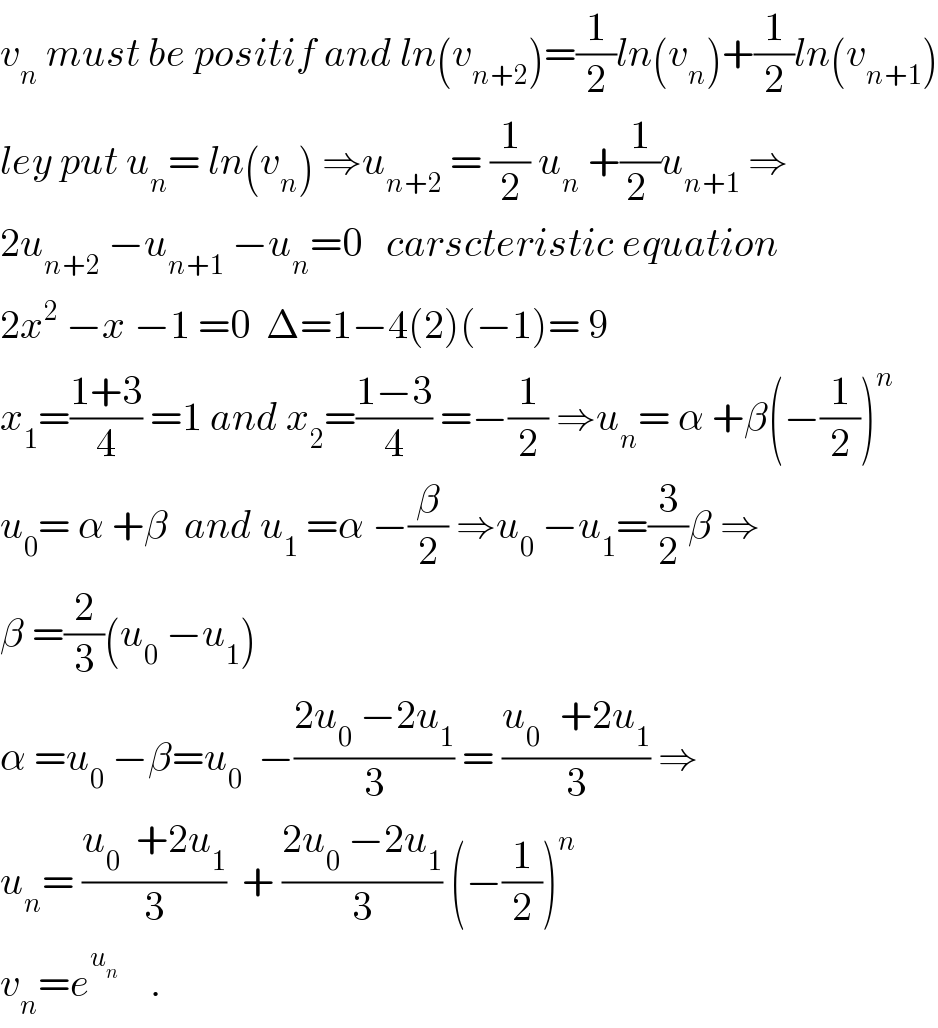
v_{n} m u s t b e p o s i t i f a n d l n (v_{n + 2}) = \frac{1}{2} l n (v_{n}) + \frac{1}{2} l n (v_{n + 1})

l e y p u t u_{n} = l n (v_{n}) \Rightarrow u_{n + 2} = \frac{1}{2} u_{n} + \frac{1}{2} u_{n + 1} \Rightarrow

2 u_{n + 2} - u_{n + 1} - u_{n} = 0 c a r s c t e r i s t i c e q u a t i o n

2 x^{2} - x - 1 = 0 Δ = 1 - 4 (2) (- 1) = 9

x_{1} = \frac{1 + 3}{4} = 1 a n d x_{2} = \frac{1 - 3}{4} = - \frac{1}{2} \Rightarrow u_{n} = α + β {(- \frac{1}{2})}^{n}

u_{0} = α + β a n d u_{1} = α - \frac{β}{2} \Rightarrow u_{0} - u_{1} = \frac{3}{2} β \Rightarrow

β = \frac{2}{3} (u_{0} - u_{1})

α = u_{0} - β = u_{0} - \frac{2 u_{0} - 2 u_{1}}{3} = \frac{u_{0} + 2 u_{1}}{3} \Rightarrow

u_{n} = \frac{u_{0} + 2 u_{1}}{3} + \frac{2 u_{0} - 2 u_{1}}{3} {(- \frac{1}{2})}^{n}

v_{n} = e^{u_{n}} .