Question Number 185036 by Mastermind last updated on 16/Jan/23
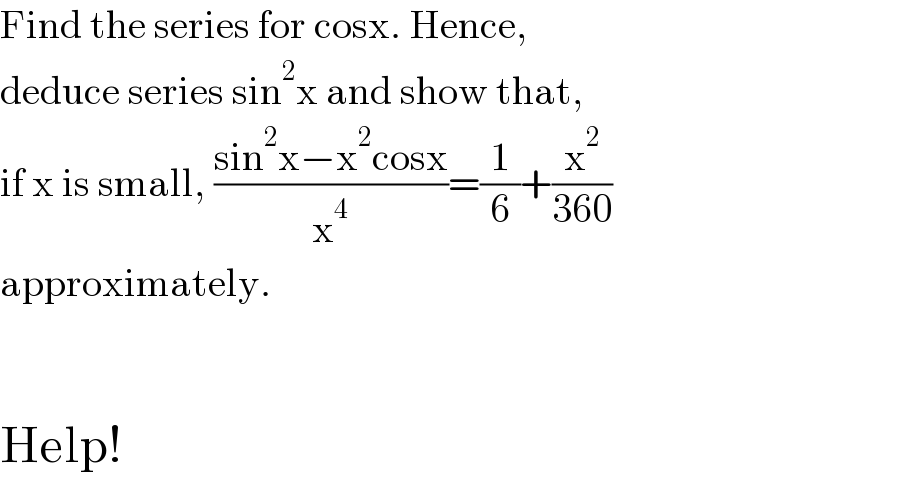
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{series}\:\mathrm{for}\:\mathrm{cosx}.\:\mathrm{Hence},\: \\ $$$$\mathrm{deduce}\:\mathrm{series}\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{and}\:\mathrm{show}\:\mathrm{that}, \\ $$$$\mathrm{if}\:\mathrm{x}\:\mathrm{is}\:\mathrm{small},\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{x}^{\mathrm{2}} \mathrm{cosx}}{\mathrm{x}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{360}} \\ $$$$\mathrm{approximately}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$
Answered by aba last updated on 16/Jan/23
![cos(x)=Σ_(n=0) ^∞ (((−1)^n x^(2n) )/((2n)! )) sin^2 (x)=((1−cos(2x))/2)=(1/2)[1−Σ_(n=0) ^∞ (((−1)^n (2x)^(2n) )/((2n)!))]](https://www.tinkutara.com/question/Q185060.png)
$$\mathrm{cos}\left(\mathrm{x}\right)=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!\:}\: \\ $$$$\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)=\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}−\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{2x}\right)^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}\right] \\ $$
