Menu Close

Find-the-shortest-distance-between-the-curves-9x-2-9y-2-30y-16-0-and-y-2-x-3-

Tinku Tara 0 Comments
Pin




Question Number 37777 by rahul 19 last updated on 17/Jun/18
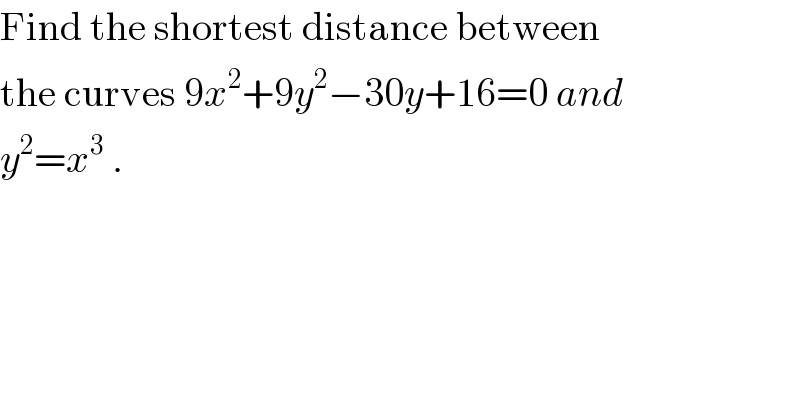
Find the shortest distance between the curves 9x^2 +9y^2 −30y+16=0 and y^2 =x^3 .
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{shortest}\:\mathrm{distance}\:\mathrm{between} \\ $$$$\mathrm{the}\:\mathrm{curves}\:\mathrm{9}{x}^{\mathrm{2}} +\mathrm{9}{y}^{\mathrm{2}} −\mathrm{30}{y}+\mathrm{16}=\mathrm{0}\:{and} \\ $$$${y}^{\mathrm{2}} ={x}^{\mathrm{3}} \:. \\ $$
Answered by MJS last updated on 17/Jun/18
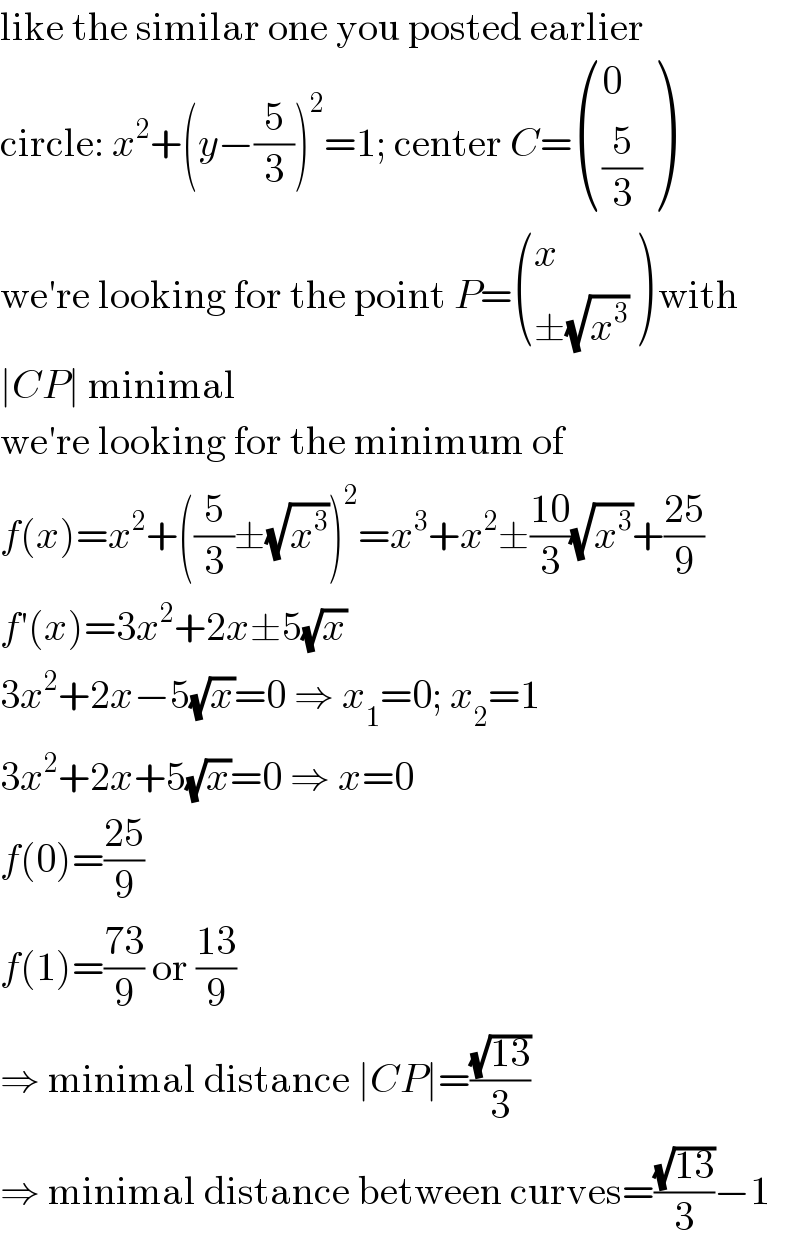
like the similar one you posted earlier circle: x^2 +(y−(5/3))^2 =1; center C= ((0),((5/3)) ) we′re looking for the point P= ((x),((±(√x^3 ))) ) with ∣CP∣ minimal we′re looking for the minimum of f(x)=x^2 +((5/3)±(√x^3 ))^2 =x^3 +x^2 ±((10)/3)(√x^3 )+((25)/9) f′(x)=3x^2 +2x±5(√x) 3x^2 +2x−5(√x)=0 ⇒ x_1 =0; x_2 =1 3x^2 +2x+5(√x)=0 ⇒ x=0 f(0)=((25)/9) f(1)=((73)/9) or ((13)/9) ⇒ minimal distance ∣CP∣=((√(13))/3) ⇒ minimal distance between curves=((√(13))/3)−1
$$\mathrm{like}\:\mathrm{the}\:\mathrm{similar}\:\mathrm{one}\:\mathrm{you}\:\mathrm{posted}\:\mathrm{earlier} \\ $$$$\mathrm{circle}:\:{x}^{\mathrm{2}} +\left({y}−\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{2}} =\mathrm{1};\:\mathrm{center}\:{C}=\begin{pmatrix}{\mathrm{0}}\\{\frac{\mathrm{5}}{\mathrm{3}}}\end{pmatrix} \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{the}\:\mathrm{point}\:{P}=\begin{pmatrix}{{x}}\\{\pm\sqrt{{x}^{\mathrm{3}} }}\end{pmatrix}\:\mathrm{with} \\ $$$$\mid{CP}\mid\:\mathrm{minimal} \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of} \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} +\left(\frac{\mathrm{5}}{\mathrm{3}}\pm\sqrt{{x}^{\mathrm{3}} }\right)^{\mathrm{2}} ={x}^{\mathrm{3}} +{x}^{\mathrm{2}} \pm\frac{\mathrm{10}}{\mathrm{3}}\sqrt{{x}^{\mathrm{3}} }+\frac{\mathrm{25}}{\mathrm{9}} \\ $$$${f}'\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}\pm\mathrm{5}\sqrt{{x}} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{5}\sqrt{{x}}=\mathrm{0}\:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{0};\:{x}_{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\sqrt{{x}}=\mathrm{0}\:\Rightarrow\:{x}=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)=\frac{\mathrm{25}}{\mathrm{9}} \\ $$$${f}\left(\mathrm{1}\right)=\frac{\mathrm{73}}{\mathrm{9}}\:\mathrm{or}\:\frac{\mathrm{13}}{\mathrm{9}} \\ $$$$\Rightarrow\:\mathrm{minimal}\:\mathrm{distance}\:\mid{CP}\mid=\frac{\sqrt{\mathrm{13}}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{minimal}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{curves}=\frac{\sqrt{\mathrm{13}}}{\mathrm{3}}−\mathrm{1} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18
excellent sir
$${excellent}\:{sir} \\ $$
Commented by MJS last updated on 17/Jun/18
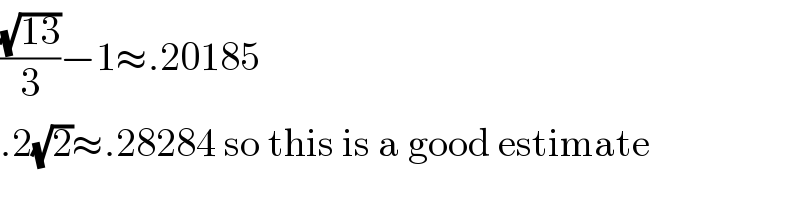
((√(13))/3)−1≈.20185 .2(√2)≈.28284 so this is a good estimate
$$\frac{\sqrt{\mathrm{13}}}{\mathrm{3}}−\mathrm{1}\approx.\mathrm{20185} \\ $$$$.\mathrm{2}\sqrt{\mathrm{2}}\approx.\mathrm{28284}\:\mathrm{so}\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{good}\:\mathrm{estimate} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18
shortest distance...see(0.8,1) lies on circle... distance from (0.8,1)≈half diagonal of the smallest squre (1/2)×(√((0.2)^2 +(0.2)^2 )) ....pls comment
$${shortest}\:{distance}…{see}\left(\mathrm{0}.\mathrm{8},\mathrm{1}\right)\:{lies}\:{on}\:{circle}… \\ $$$${distance}\:{from}\:\left(\mathrm{0}.\mathrm{8},\mathrm{1}\right)\approx{half}\:{diagonal}\:{of}\:{the} \\ $$$${smallest}\:{squre}\:\:\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\left(\mathrm{0}.\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{0}.\mathrm{2}\right)^{\mathrm{2}} }\:….{pls}\:{comment} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *