Menu Close

Find-the-shotest-distance-between-the-line-x-8-3-y-2-4-z-1-1-x-3-3-y-4-5-z-2-2-

Tinku Tara 0 Comments
Pin




Question Number 56711 by Tawa1 last updated on 22/Mar/19
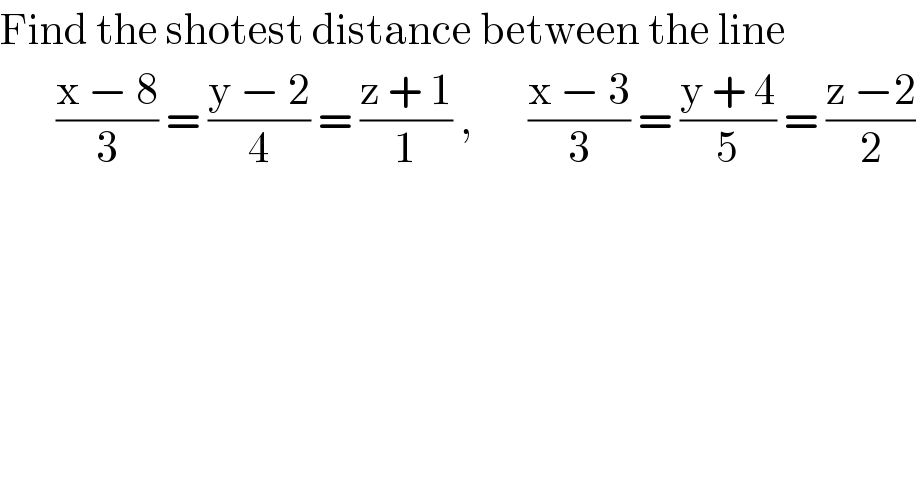
Find the shotest distance between the line ((x − 8)/3) = ((y − 2)/4) = ((z + 1)/1) , ((x − 3)/3) = ((y + 4)/5) = ((z −2)/2)
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{shotest}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{the}\:\mathrm{line} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{x}\:−\:\mathrm{8}}{\mathrm{3}}\:=\:\frac{\mathrm{y}\:−\:\mathrm{2}}{\mathrm{4}}\:=\:\frac{\mathrm{z}\:+\:\mathrm{1}}{\mathrm{1}}\:,\:\:\:\:\:\:\:\frac{\mathrm{x}\:−\:\mathrm{3}}{\mathrm{3}}\:=\:\frac{\mathrm{y}\:+\:\mathrm{4}}{\mathrm{5}}\:=\:\frac{\mathrm{z}\:−\mathrm{2}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 23/Mar/19
using vector method: L1: (8,2,−1)+s(3,4,1) L2: (3,−4,2)+t(3,5,2) normal to L1 and L2: (3,4,1)×(3,5,2)=(3,−3,3) unit normal: (3,−3,3)/(√(3^2 +(−3)^2 +3^2 ))=((1/( (√3))),−(1/( (√3))),(1/( (√3)))) d=∣(8−3,2+4,−1−2)•((1/( (√3))),−(1/( (√3))),(1/( (√3))))∣ d=∣(5,6,−3)•(1,−1,1)∣/(√3) d=∣−4∣/(√3) ⇒d=(4/( (√3)))≈2.309
$${using}\:{vector}\:{method}: \\ $$$$ \\ $$$${L}\mathrm{1}:\:\left(\mathrm{8},\mathrm{2},−\mathrm{1}\right)+{s}\left(\mathrm{3},\mathrm{4},\mathrm{1}\right) \\ $$$${L}\mathrm{2}:\:\left(\mathrm{3},−\mathrm{4},\mathrm{2}\right)+{t}\left(\mathrm{3},\mathrm{5},\mathrm{2}\right) \\ $$$${normal}\:{to}\:{L}\mathrm{1}\:{and}\:{L}\mathrm{2}: \\ $$$$\left(\mathrm{3},\mathrm{4},\mathrm{1}\right)×\left(\mathrm{3},\mathrm{5},\mathrm{2}\right)=\left(\mathrm{3},−\mathrm{3},\mathrm{3}\right) \\ $$$${unit}\:{normal}: \\ $$$$\left(\mathrm{3},−\mathrm{3},\mathrm{3}\right)/\sqrt{\mathrm{3}^{\mathrm{2}} +\left(−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}},−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}},\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$${d}=\mid\left(\mathrm{8}−\mathrm{3},\mathrm{2}+\mathrm{4},−\mathrm{1}−\mathrm{2}\right)\bullet\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}},−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}},\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\mid \\ $$$${d}=\mid\left(\mathrm{5},\mathrm{6},−\mathrm{3}\right)\bullet\left(\mathrm{1},−\mathrm{1},\mathrm{1}\right)\mid/\sqrt{\mathrm{3}} \\ $$$${d}=\mid−\mathrm{4}\mid/\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{d}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\approx\mathrm{2}.\mathrm{309} \\ $$
Commented by Tawa1 last updated on 26/Mar/19
I appreciate your effort sir
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *