Question Number 91476 by Zainal Arifin last updated on 01/May/20

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{slope}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tangent}\: \\ $$$$\mathrm{line}\:\mathrm{to}\:\mathrm{the}\:\mathrm{graph}\:\mathrm{of}: \\ $$$$\mathrm{y}^{\mathrm{4}} +\mathrm{3y}−\mathrm{4x}^{\mathrm{3}} =\mathrm{5x}+\mathrm{1}\:\:\mathrm{at}\:\mathrm{the}\:\mathrm{point} \\ $$$$\mathrm{P}\:\left(\mathrm{1},\:−\mathrm{2}\right) \\ $$
Commented by john santu last updated on 01/May/20
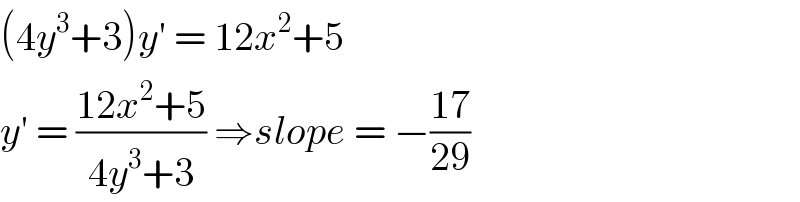
$$\left(\mathrm{4}{y}^{\mathrm{3}} +\mathrm{3}\right){y}'\:=\:\mathrm{12}{x}^{\mathrm{2}} +\mathrm{5} \\ $$$${y}'\:=\:\frac{\mathrm{12}{x}^{\mathrm{2}} +\mathrm{5}}{\mathrm{4}{y}^{\mathrm{3}} +\mathrm{3}}\:\Rightarrow{slope}\:=\:−\frac{\mathrm{17}}{\mathrm{29}} \\ $$
Commented by Zainal Arifin last updated on 01/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:,\:\mathrm{you}\:\mathrm{are}\:\mathrm{right}. \\ $$
