find-the-smallest-integer-which-has-28-divisors-and-is-divisible-by-28-

Question Number 124567 by mr W last updated on 04/Dec/20

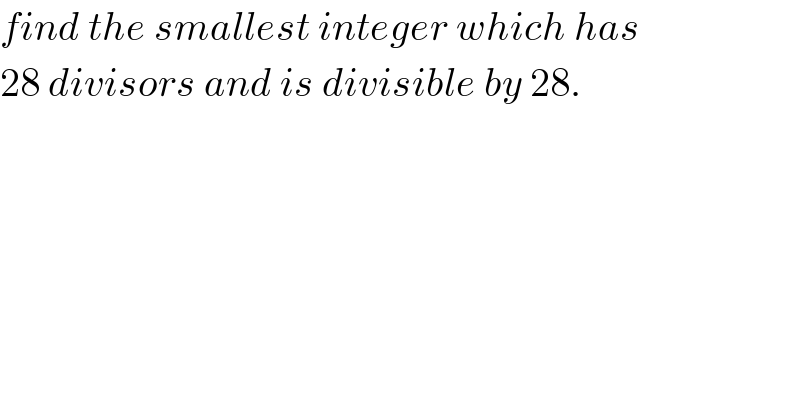
f i n d t h e s m a l l e s t i n t e g e r w h i c h h a s

28 d i v i s o r s a n d i s d i v i s i b l e b y 28 .

Answered by mr W last updated on 05/Dec/20

s a y t h e n u m b e r i s n = p^{a} q^{b} r^{c} \dots

(a + 1) (b + 1) (c + 1) \dots = 28

= 28 \times 1 \Rightarrow a = 27 \Rightarrow n = p^{27} \dots (i)

= 14 \times 2 \Rightarrow a = 13, b = 1 \Rightarrow n = p^{13} q^{1} \dots (i i)

= 7 \times 4 \Rightarrow a = 6, b = 3 \Rightarrow n = p^{6} q^{3} \dots (i i i)

= 7 \times 2 \times 2 \Rightarrow a = 6, b = 1, c = 1 \Rightarrow n = p^{6} q^{1} r^{1} \dots (i v)

28 = 2^{2} \times 7^{1}

s u c h t h a t n i s d i v i s i b l e b y 28, n m u s t

c o n t a i n a t l e a s t 2^{⩾ 2} 7^{⩾ 1}

c a s e (i) :

i m p o s s i b l e

c a s e (i i) :

n_{m i n} = 2^{13} \times 7^{1} = 57344

c a s e (i i i) :

n_{m i n} = 2^{6} \times 7^{3} = 21952

c a s e (i v) :

n_{m i n} = 2^{6} \times 3^{1} \times 7^{1} = 1344

\Rightarrow t h e n u m b e r i s 1344 .

Facebook Tweet Pin