Question Number 13154 by tawa tawa last updated on 15/May/17

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{number}\:\mathrm{such}\:\mathrm{that}\:\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{18}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{17}, \\ $$$$\mathrm{When}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{20}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\mathrm{19}.\:\mathrm{and}\:\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{24}\:\mathrm{the}\:\mathrm{remainder}\: \\ $$$$\mathrm{is}\:\mathrm{23}.\: \\ $$
Answered by mrW1 last updated on 15/May/17

$${N}=\mathrm{18}{i}+\mathrm{17}=\mathrm{20}{j}+\mathrm{19}=\mathrm{24}{k}+\mathrm{23} \\ $$$$\mathrm{20}{j}+\mathrm{19}=\mathrm{18}{j}+\mathrm{18}+\mathrm{2}{j}+\mathrm{1}=\mathrm{18}{i}+\mathrm{17} \\ $$$$\Rightarrow\mathrm{18}\left({j}−{i}\right)+\mathrm{2}{j}+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{9}\left({j}−{i}\right)+{j}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{j}+\mathrm{1}=\mathrm{9}{i}' \\ $$$$\Rightarrow{j}=\mathrm{9}{i}'−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{20}\left(\mathrm{9}{i}'−\mathrm{1}\right)+\mathrm{19}=\mathrm{24}{k}+\mathrm{23} \\ $$$$\mathrm{20}×\mathrm{9}{i}'=\mathrm{24}\left({k}+\mathrm{1}\right) \\ $$$$\mathrm{5}×\mathrm{3}{i}'=\mathrm{2}\left({k}+\mathrm{1}\right) \\ $$$$\Rightarrow{i}'=\mathrm{2}{n} \\ $$$$\Rightarrow{k}=\mathrm{15}{n}−\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow{N}=\mathrm{24}\left(\mathrm{15}{n}−\mathrm{1}\right)+\mathrm{23}=\mathrm{360}{n}−\mathrm{1}\:\:\left({n}=\mathrm{1},\mathrm{2},\mathrm{3}…\right) \\ $$$${The}\:{number}\:{is}\:\mathrm{359}\:{or}\:\mathrm{719}\:{or}… \\ $$
Commented by RasheedSindhi last updated on 15/May/17
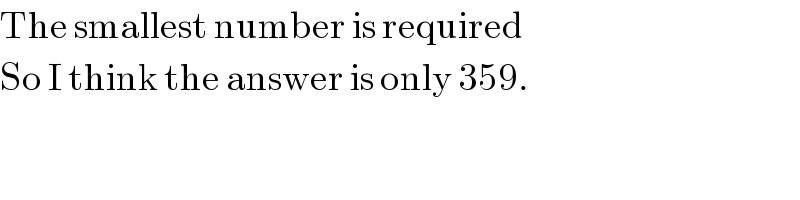
$$\mathrm{The}\:\mathrm{smallest}\:\mathrm{number}\:\mathrm{is}\:\mathrm{required} \\ $$$$\mathrm{So}\:\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{only}\:\mathrm{359}. \\ $$
Commented by tawa tawa last updated on 15/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by RasheedSindhi last updated on 15/May/17

$$\ast\mathrm{Common}\:\mathrm{diffefence}\:\mathrm{of}\:\mathrm{divisor} \\ $$$$\mathrm{and}\:\mathrm{its}\:\mathrm{remainder} \\ $$$$\:\:\:\:=\mathrm{18}−\mathrm{17}=\mathrm{20}−\mathrm{19}=\mathrm{24}−\mathrm{23}=\mathrm{1} \\ $$$$\:\ast\mathrm{lcm}\:\mathrm{of}\:\mathrm{divisors}\:\mathrm{18},\mathrm{20},\mathrm{24}\:: \\ $$$$\:\mathrm{18}=\mathrm{2}.\mathrm{3}^{\mathrm{2}} \\ $$$$\:\mathrm{20}=\mathrm{2}^{\mathrm{2}} .\mathrm{5} \\ $$$$\:\mathrm{24}=\mathrm{2}^{\mathrm{3}} .\mathrm{3} \\ $$$$\mathrm{lcm}\:\mathrm{is}\:\mathrm{2}^{\mathrm{3}} .\mathrm{3}^{\mathrm{2}} .\mathrm{5}=\mathrm{360} \\ $$$$ \\ $$$$\ast\mathrm{lcm}-\left(\mathrm{common}\:\mathrm{diff}.\:\mathrm{of}\:\mathrm{divisor}\:\&\mathrm{remainder}\right)\mathrm{u} \\ $$$$=\mathrm{360}−\mathrm{1}=\mathrm{359} \\ $$$$ \\ $$
Commented by tawa tawa last updated on 15/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mrW1 last updated on 16/May/17

$${That}'{s}\:{smart}! \\ $$
