Menu Close

find-the-solution-set-of-inequality-x-2-9-x-2-x-x-2-2-0-

Tinku Tara 0 Comments
Pin




Question Number 100385 by bobhans last updated on 26/Jun/20
find the solution set of inequality (((x^2 −9)(√(x+2)))/(x+(√((x+2)^2 )))) ≤ 0
findthesolutionsetofinequality(x2−9)x+2x+(x+2)2⩽0
Commented by bobhans last updated on 26/Jun/20
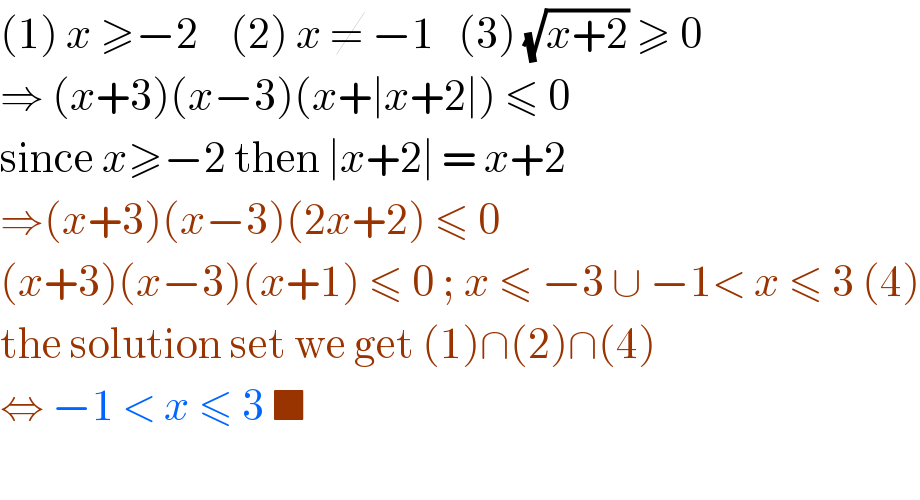
(1) x ≥−2 (2) x ≠ −1 (3) (√(x+2)) ≥ 0 ⇒ (x+3)(x−3)(x+∣x+2∣) ≤ 0 since x≥−2 then ∣x+2∣ = x+2 ⇒(x+3)(x−3)(2x+2) ≤ 0 (x+3)(x−3)(x+1) ≤ 0 ; x ≤ −3 ∪ −1< x ≤ 3 (4) the solution set we get (1)∩(2)∩(4) ⇔ −1 < x ≤ 3 ■
(1)x⩾−2(2)x≠−1(3)x+2⩾0⇒(x+3)(x−3)(x+∣x+2∣)⩽0sincex⩾−2then∣x+2∣=x+2⇒(x+3)(x−3)(2x+2)⩽0(x+3)(x−3)(x+1)⩽0;x⩽−3∪−1<x⩽3(4)thesolutionsetweget(1)∩(2)∩(4)⇔−1<x⩽3◼
Commented by bemath last updated on 26/Jun/20
cooll
cooll
Answered by MJS last updated on 26/Jun/20
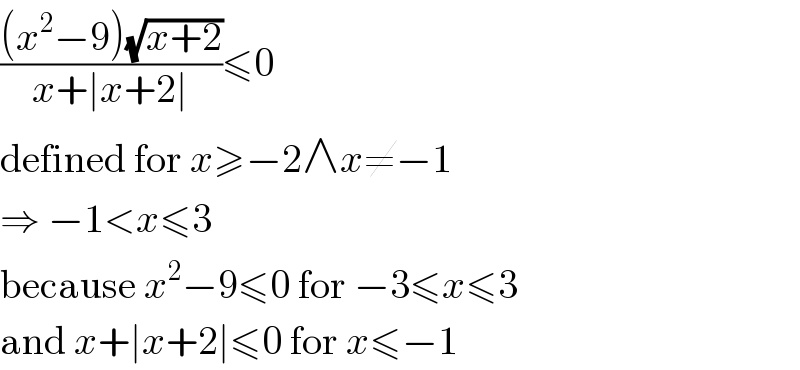
(((x^2 −9)(√(x+2)))/(x+∣x+2∣))≤0 defined for x≥−2∧x≠−1 ⇒ −1<x≤3 because x^2 −9≤0 for −3≤x≤3 and x+∣x+2∣≤0 for x≤−1
(x2−9)x+2x+∣x+2∣⩽0definedforx⩾−2∧x≠−1⇒−1<x⩽3becausex2−9⩽0for−3⩽x⩽3andx+∣x+2∣⩽0forx⩽−1
Commented by bemath last updated on 26/Jun/20
great prof. thank much
greatprof.thankmuch

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *