Question Number 19053 by Tinkutara last updated on 03/Aug/17
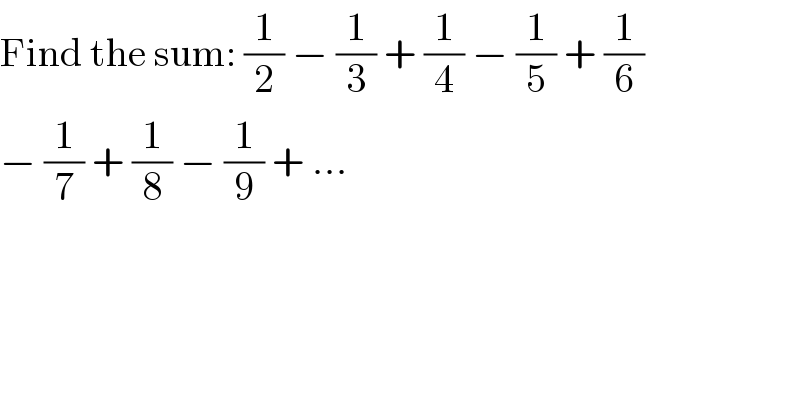
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}:\:\frac{\mathrm{1}}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\:−\:\frac{\mathrm{1}}{\mathrm{5}}\:+\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$−\:\frac{\mathrm{1}}{\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{8}}\:−\:\frac{\mathrm{1}}{\mathrm{9}}\:+\:… \\ $$
Answered by ajfour last updated on 03/Aug/17
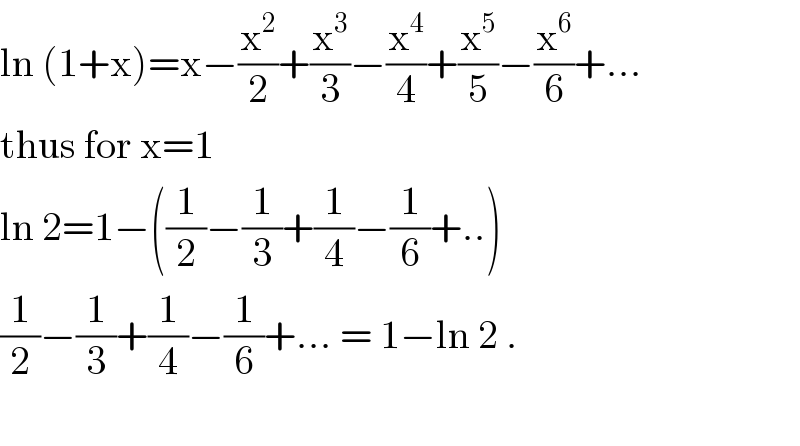
$$\mathrm{ln}\:\left(\mathrm{1}+\mathrm{x}\right)=\mathrm{x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}}+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{5}}−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{6}}+… \\ $$$$\mathrm{thus}\:\mathrm{for}\:\mathrm{x}=\mathrm{1} \\ $$$$\mathrm{ln}\:\mathrm{2}=\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{6}}+..\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{6}}+…\:=\:\mathrm{1}−\mathrm{ln}\:\mathrm{2}\:. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 03/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
