Question Number 96317 by M±th+et+s last updated on 31/May/20
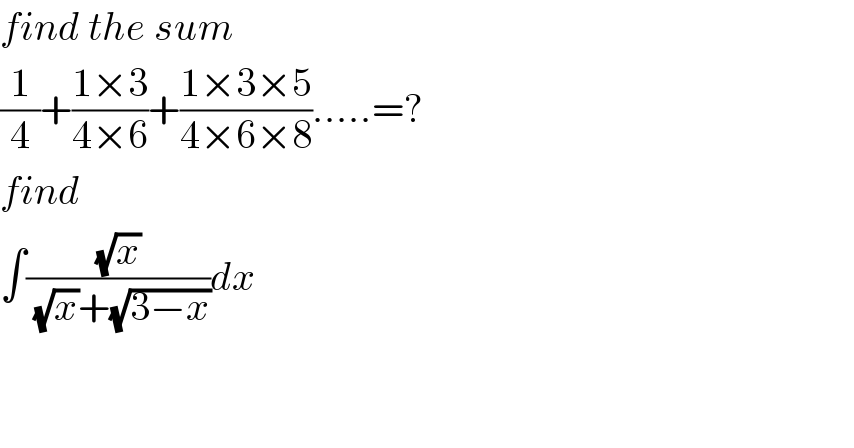
$${find}\:{the}\:{sum} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}×\mathrm{3}}{\mathrm{4}×\mathrm{6}}+\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}}{\mathrm{4}×\mathrm{6}×\mathrm{8}}…..=? \\ $$$${find} \\ $$$$\int\frac{\sqrt{{x}}}{\:\sqrt{{x}}+\sqrt{\mathrm{3}−{x}}}{dx} \\ $$$$ \\ $$$$ \\ $$
Commented by bemath last updated on 01/Jun/20
![(2) ∫ (((√x) dx )/( (√x)(1+(√((3/x)−1)))))= ∫ (dx/(1+(√((3/x)−1)))) ; [ (3/x)−1= z^2 ] x = (3/(z^2 +1)) ⇒dx = ((−6z)/((z^2 +1)^2 )) dz ∫ ((−6z dz)/((z^2 +1)^2 (1+z))) = −(3/2)∫( (1/(z+1))−((z+1)/(z^2 +1))−((2z−2)/((z^2 +1)^2 ))) dz = −(3/4)[2ln∣(√((3−x)/x))∣ + ln ∣(x/3)∣ +((2x)/3) ((√((3−x)/x))+2)] + c](https://www.tinkutara.com/question/Q96376.png)
$$\left(\mathrm{2}\right)\:\int\:\frac{\sqrt{\mathrm{x}}\:\mathrm{dx}\:}{\:\sqrt{\mathrm{x}}\left(\mathrm{1}+\sqrt{\frac{\mathrm{3}}{\mathrm{x}}−\mathrm{1}}\right)}= \\ $$$$\int\:\frac{\mathrm{dx}}{\mathrm{1}+\sqrt{\frac{\mathrm{3}}{\mathrm{x}}−\mathrm{1}}}\:;\:\:\left[\:\frac{\mathrm{3}}{\mathrm{x}}−\mathrm{1}=\:\mathrm{z}^{\mathrm{2}} \right]\: \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{3}}{\mathrm{z}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow\mathrm{dx}\:=\:\frac{−\mathrm{6z}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dz}\: \\ $$$$\int\:\frac{−\mathrm{6z}\:\mathrm{dz}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{z}\right)}\:=\:−\frac{\mathrm{3}}{\mathrm{2}}\int\left(\:\frac{\mathrm{1}}{\mathrm{z}+\mathrm{1}}−\frac{\mathrm{z}+\mathrm{1}}{\mathrm{z}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{2z}−\mathrm{2}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right)\:\mathrm{dz} \\ $$$$=\:−\frac{\mathrm{3}}{\mathrm{4}}\left[\mathrm{2ln}\mid\sqrt{\frac{\mathrm{3}−\mathrm{x}}{\mathrm{x}}}\mid\:+\:\mathrm{ln}\:\mid\frac{\mathrm{x}}{\mathrm{3}}\mid\:+\frac{\mathrm{2x}}{\mathrm{3}}\:\left(\sqrt{\frac{\mathrm{3}−\mathrm{x}}{\mathrm{x}}}+\mathrm{2}\right)\right]\:+\:\mathrm{c}\: \\ $$
