Question Number 89313 by abdomathmax last updated on 16/Apr/20
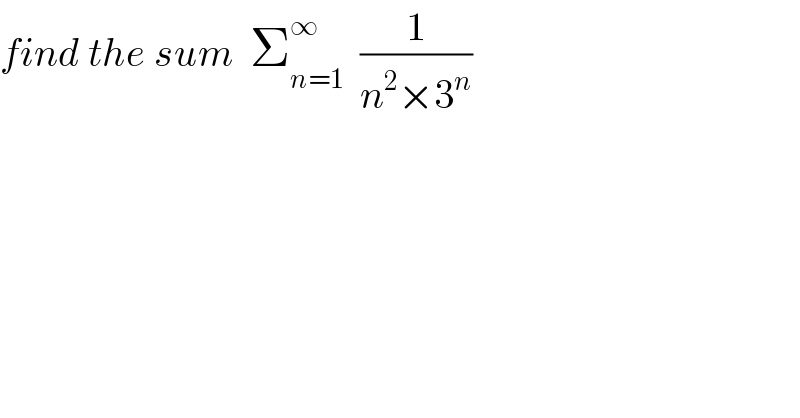
$${find}\:{the}\:{sum}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} ×\mathrm{3}^{{n}} } \\ $$
Commented by mathmax by abdo last updated on 19/Apr/20
![let find s(x)=Σ_(n=1) ^∞ (x^n /n^2 ) with ∣x∣<1 we have Σ_(n=0) ^∞ x^n =(1/(1−x)) ⇒Σ_(n=0) ^∞ (x^(n+1) /(n+1)) =−ln(1−x) ⇒ Σ_(n=1) ^∞ (x^n /n) =−ln(1−x)⇒Σ_(n=1) ^∞ (x^(n−1) /n) =−((ln(1−x))/x) ⇒ Σ_(n=1) ^∞ (x^n /n^2 ) =−∫((ln(1−x))/x)dx +c =−∫_0 ^x ((ln(1−t))/t) dt +c s(x) =c−∫_0 ^x ((ln(1−t))/t)dt s(0)=0 =c ⇒s(x) =−∫_0 ^x ((ln(1−t))/t)dt ⇒ Σ_(n=1) ^∞ (1/(n^2 ×3^n )) =s((1/3))=−∫_0 ^(1/3) ((ln(1−t))/t)dt =_(u=3t) −3∫_0 ^1 ((ln(1−(u/3)))/u)×(du/3) =−∫_0 ^1 ((ln(1−(u/3)))/u) du (u/3) =cosθ give Σ(...)=−∫_(π/2) ^(arcos((1/3))) ((ln(1−cosθ))/(3cosθ))(−3sinθ)dθ =∫_(π/2) ^(arcos((1/3))) tanθln(2sin^2 ((θ/(2 ))))dθ =ln(2)∫_(π/2) ^(arcos((1/3))) tanθ dθ+2 ∫_(π/2) ^(arcos((1/3))) tanθ ln(sin((θ/2)))dθ ∫_(π/2) ^(arcos((1/3))) tanθ dθ =−ln∣cosθ∣]_(π/2) ^(arcos((1/3))) =−ln((1/3))=ln(3) ....be continued....](https://www.tinkutara.com/question/Q89828.png)
$${let}\:{find}\:{s}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}^{\mathrm{2}} }\:\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$$${we}\:{have}\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=−{ln}\left(\mathrm{1}−{x}\right)\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:=−{ln}\left(\mathrm{1}−{x}\right)\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}−\mathrm{1}} }{{n}}\:=−\frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}^{\mathrm{2}} }\:=−\int\frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx}\:+{c}\:=−\int_{\mathrm{0}} ^{{x}} \:\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}\:{dt}\:+{c} \\ $$$${s}\left({x}\right)\:={c}−\int_{\mathrm{0}} ^{{x}} \:\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$${s}\left(\mathrm{0}\right)=\mathrm{0}\:={c}\:\Rightarrow{s}\left({x}\right)\:=−\int_{\mathrm{0}} ^{{x}} \:\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} ×\mathrm{3}^{{n}} }\:={s}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=−\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$$=_{{u}=\mathrm{3}{t}} \:\:\:\:\:−\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−\frac{{u}}{\mathrm{3}}\right)}{{u}}×\frac{{du}}{\mathrm{3}}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−\frac{{u}}{\mathrm{3}}\right)}{{u}}\:{du} \\ $$$$\frac{{u}}{\mathrm{3}}\:={cos}\theta\:\:{give}\:\Sigma\left(…\right)=−\int_{\frac{\pi}{\mathrm{2}}} ^{{arcos}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} \:\frac{{ln}\left(\mathrm{1}−{cos}\theta\right)}{\mathrm{3}{cos}\theta}\left(−\mathrm{3}{sin}\theta\right){d}\theta \\ $$$$=\int_{\frac{\pi}{\mathrm{2}}} ^{{arcos}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} {tan}\theta{ln}\left(\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}\:}\right)\right){d}\theta \\ $$$$={ln}\left(\mathrm{2}\right)\int_{\frac{\pi}{\mathrm{2}}} ^{{arcos}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} {tan}\theta\:{d}\theta+\mathrm{2}\:\int_{\frac{\pi}{\mathrm{2}}} ^{{arcos}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} \:{tan}\theta\:{ln}\left({sin}\left(\frac{\theta}{\mathrm{2}}\right)\right){d}\theta \\ $$$$\left.\int_{\frac{\pi}{\mathrm{2}}} ^{{arcos}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} \:\:{tan}\theta\:{d}\theta\:=−{ln}\mid{cos}\theta\mid\right]_{\frac{\pi}{\mathrm{2}}} ^{{arcos}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} =−{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)={ln}\left(\mathrm{3}\right) \\ $$$$….{be}\:{continued}…. \\ $$$$ \\ $$
