Menu Close

Find-the-sum-of-n-terms-of-the-series-S-n-1-22-333-4444-

Tinku Tara 0 Comments
Pin




Question Number 121235 by ZiYangLee last updated on 06/Nov/20
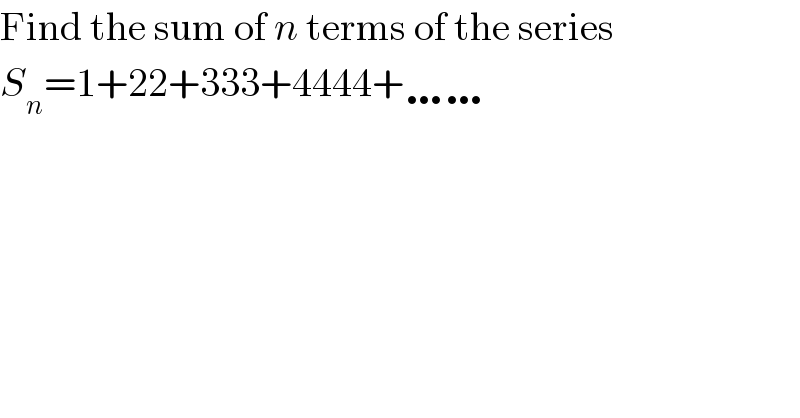
Find the sum of n terms of the series S_n =1+22+333+4444+……
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:{n}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{series} \\ $$$${S}_{{n}} =\mathrm{1}+\mathrm{22}+\mathrm{333}+\mathrm{4444}+\ldots\ldots \\ $$
Answered by Ar Brandon last updated on 06/Nov/20
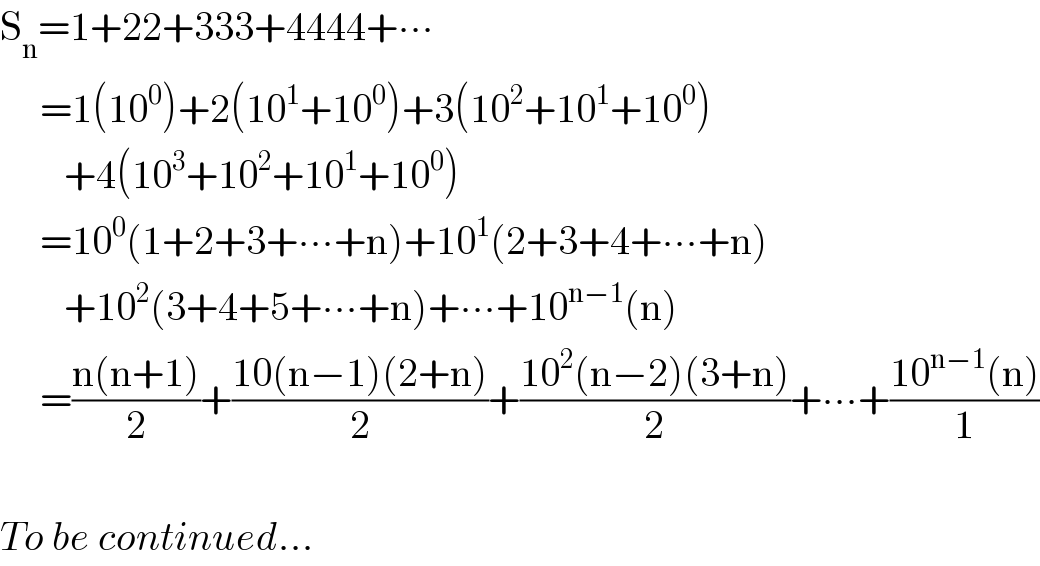
S_n =1+22+333+4444+∙∙∙ =1(10^0 )+2(10^1 +10^0 )+3(10^2 +10^1 +10^0 ) +4(10^3 +10^2 +10^1 +10^0 ) =10^0 (1+2+3+∙∙∙+n)+10^1 (2+3+4+∙∙∙+n) +10^2 (3+4+5+∙∙∙+n)+∙∙∙+10^(n−1) (n) =((n(n+1))/2)+((10(n−1)(2+n))/2)+((10^2 (n−2)(3+n))/2)+∙∙∙+((10^(n−1) (n))/1) To be continued...
$$\mathrm{S}_{\mathrm{n}} =\mathrm{1}+\mathrm{22}+\mathrm{333}+\mathrm{4444}+\centerdot\centerdot\centerdot \\ $$$$\:\:\:\:\:=\mathrm{1}\left(\mathrm{10}^{\mathrm{0}} \right)+\mathrm{2}\left(\mathrm{10}^{\mathrm{1}} +\mathrm{10}^{\mathrm{0}} \right)+\mathrm{3}\left(\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{1}} +\mathrm{10}^{\mathrm{0}} \right) \\ $$$$\:\:\:\:\:\:\:\:+\mathrm{4}\left(\mathrm{10}^{\mathrm{3}} +\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{1}} +\mathrm{10}^{\mathrm{0}} \right) \\ $$$$\:\:\:\:\:=\mathrm{10}^{\mathrm{0}} \left(\mathrm{1}+\mathrm{2}+\mathrm{3}+\centerdot\centerdot\centerdot+\mathrm{n}\right)+\mathrm{10}^{\mathrm{1}} \left(\mathrm{2}+\mathrm{3}+\mathrm{4}+\centerdot\centerdot\centerdot+\mathrm{n}\right) \\ $$$$\:\:\:\:\:\:\:\:+\mathrm{10}^{\mathrm{2}} \left(\mathrm{3}+\mathrm{4}+\mathrm{5}+\centerdot\centerdot\centerdot+\mathrm{n}\right)+\centerdot\centerdot\centerdot+\mathrm{10}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{n}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}+\frac{\mathrm{10}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{2}+\mathrm{n}\right)}{\mathrm{2}}+\frac{\mathrm{10}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{2}\right)\left(\mathrm{3}+\mathrm{n}\right)}{\mathrm{2}}+\centerdot\centerdot\centerdot+\frac{\mathrm{10}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{n}\right)}{\mathrm{1}} \\ $$$$ \\ $$$${To}\:{be}\:{continued}… \\ $$
Answered by Dwaipayan Shikari last updated on 06/Nov/20
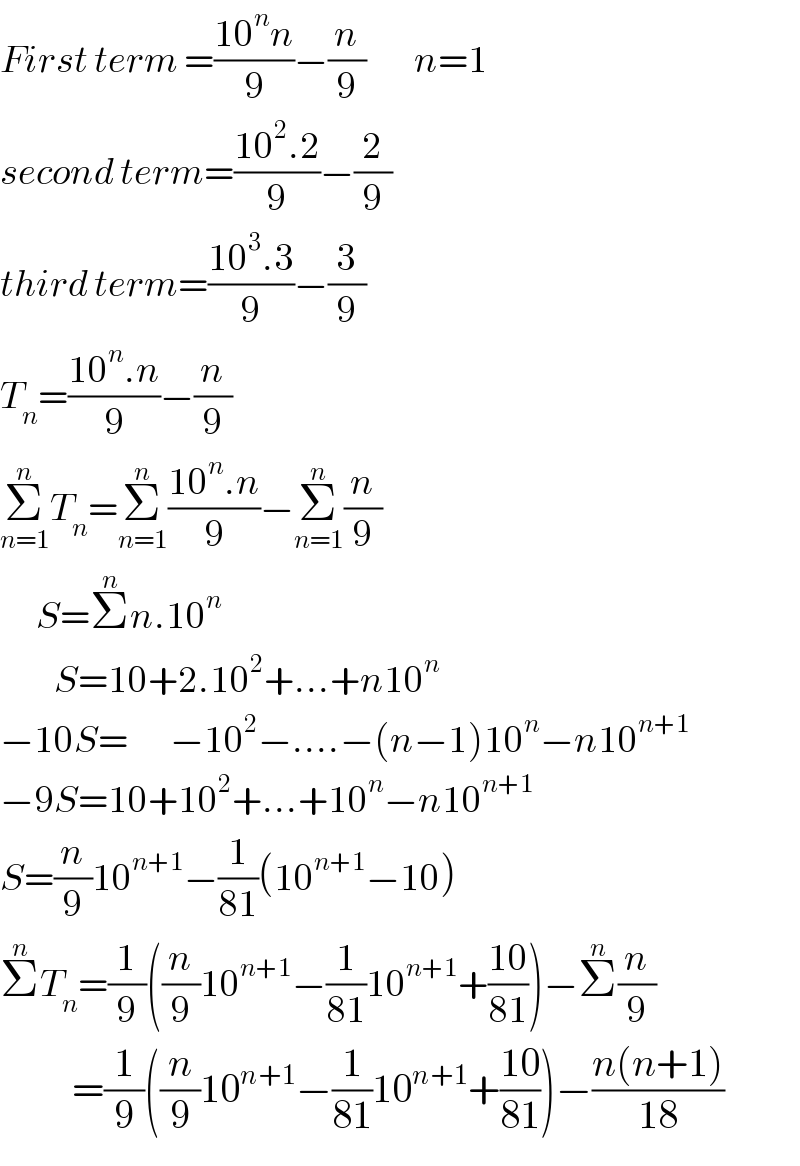
First term =((10^n n)/9)−(n/9) n=1 second term=((10^2 .2)/9)−(2/9) third term=((10^3 .3)/9)−(3/9) T_n =((10^n .n)/9)−(n/9) Σ_(n=1) ^n T_n =Σ_(n=1) ^n ((10^n .n)/9)−Σ_(n=1) ^n (n/9) S=Σ^n n.10^n S=10+2.10^2 +...+n10^n −10S= −10^2 −....−(n−1)10^n −n10^(n+1) −9S=10+10^2 +...+10^n −n10^(n+1) S=(n/9)10^(n+1) −(1/(81))(10^(n+1) −10) Σ^n T_n =(1/9)((n/9)10^(n+1) −(1/(81))10^(n+1) +((10)/(81)))−Σ^n (n/9) =(1/9)((n/9)10^(n+1) −(1/(81))10^(n+1) +((10)/(81)))−((n(n+1))/(18))
$${First}\:{term}\:=\frac{\mathrm{10}^{{n}} {n}}{\mathrm{9}}−\frac{{n}}{\mathrm{9}}\:\:\:\:\:\:\:\:{n}=\mathrm{1} \\ $$$${second}\:{term}=\frac{\mathrm{10}^{\mathrm{2}} .\mathrm{2}}{\mathrm{9}}−\frac{\mathrm{2}}{\mathrm{9}} \\ $$$${third}\:{term}=\frac{\mathrm{10}^{\mathrm{3}} .\mathrm{3}}{\mathrm{9}}−\frac{\mathrm{3}}{\mathrm{9}} \\ $$$${T}_{{n}} =\frac{\mathrm{10}^{{n}} .{n}}{\mathrm{9}}−\frac{{n}}{\mathrm{9}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{T}_{{n}} =\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{10}^{{n}} .{n}}{\mathrm{9}}−\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{n}}{\mathrm{9}} \\ $$$$\:\:\:\:\:\:{S}=\overset{{n}} {\sum}{n}.\mathrm{10}^{{n}} \\ $$$$\:\:\:\:\:\:\:\:\:{S}=\mathrm{10}+\mathrm{2}.\mathrm{10}^{\mathrm{2}} +…+{n}\mathrm{10}^{{n}} \\ $$$$−\mathrm{10}{S}=\:\:\:\:\:\:\:−\mathrm{10}^{\mathrm{2}} −….−\left({n}−\mathrm{1}\right)\mathrm{10}^{{n}} −{n}\mathrm{10}^{{n}+\mathrm{1}} \\ $$$$−\mathrm{9}{S}=\mathrm{10}+\mathrm{10}^{\mathrm{2}} +…+\mathrm{10}^{{n}} −{n}\mathrm{10}^{{n}+\mathrm{1}} \\ $$$${S}=\frac{{n}}{\mathrm{9}}\mathrm{10}^{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{81}}\left(\mathrm{10}^{{n}+\mathrm{1}} −\mathrm{10}\right) \\ $$$$\overset{{n}} {\sum}{T}_{{n}} =\frac{\mathrm{1}}{\mathrm{9}}\left(\frac{{n}}{\mathrm{9}}\mathrm{10}^{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{81}}\mathrm{10}^{{n}+\mathrm{1}} +\frac{\mathrm{10}}{\mathrm{81}}\right)−\overset{{n}} {\sum}\frac{{n}}{\mathrm{9}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{9}}\left(\frac{{n}}{\mathrm{9}}\mathrm{10}^{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{81}}\mathrm{10}^{{n}+\mathrm{1}} +\frac{\mathrm{10}}{\mathrm{81}}\right)−\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{18}} \\ $$
Commented by Dwaipayan Shikari last updated on 06/Nov/20
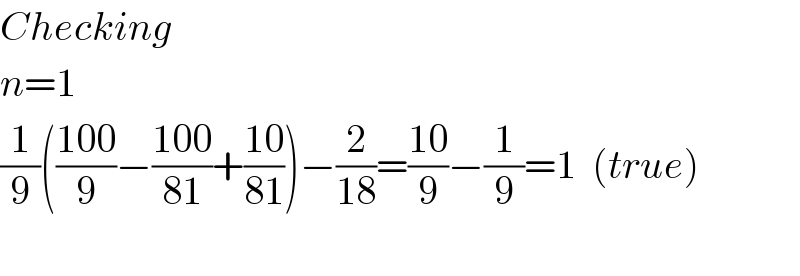
Checking n=1 (1/9)(((100)/9)−((100)/(81))+((10)/(81)))−(2/(18))=((10)/9)−(1/9)=1 (true)
$${Checking} \\ $$$${n}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{9}}\left(\frac{\mathrm{100}}{\mathrm{9}}−\frac{\mathrm{100}}{\mathrm{81}}+\frac{\mathrm{10}}{\mathrm{81}}\right)−\frac{\mathrm{2}}{\mathrm{18}}=\frac{\mathrm{10}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{9}}=\mathrm{1}\:\:\left({true}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *