Question Number 124332 by ZiYangLee last updated on 02/Dec/20

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{all}\:\mathrm{positive}\:\mathrm{integers} \\ $$$$\mathrm{of}\:\mathrm{all}\:\mathrm{positive}\:\mathrm{factorsof}\:\mathrm{12} \\ $$
Answered by mr W last updated on 02/Dec/20
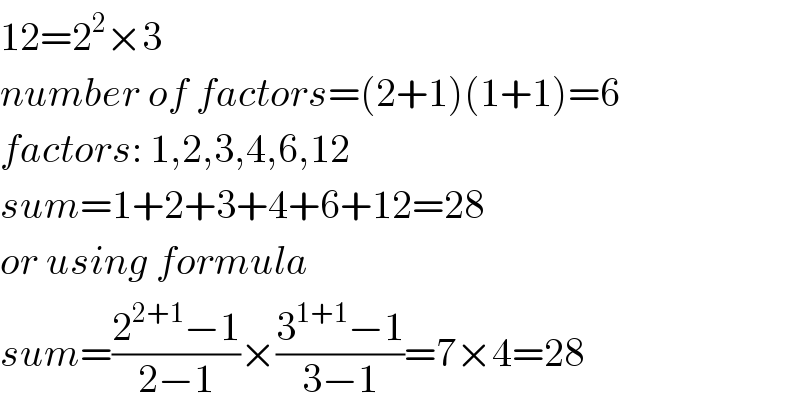
$$\mathrm{12}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3} \\ $$$${number}\:{of}\:{factors}=\left(\mathrm{2}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)=\mathrm{6} \\ $$$${factors}:\:\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{6},\mathrm{12} \\ $$$${sum}=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{6}+\mathrm{12}=\mathrm{28} \\ $$$${or}\:{using}\:{formula} \\ $$$${sum}=\frac{\mathrm{2}^{\mathrm{2}+\mathrm{1}} −\mathrm{1}}{\mathrm{2}−\mathrm{1}}×\frac{\mathrm{3}^{\mathrm{1}+\mathrm{1}} −\mathrm{1}}{\mathrm{3}−\mathrm{1}}=\mathrm{7}×\mathrm{4}=\mathrm{28} \\ $$
