Find-the-sum-to-n-term-1-2-3-4-5-6-7-8-9-

Question Number 147878 by Tawa11 last updated on 24/Jul/21

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{to}\:\:\mathrm{n}\:\:\mathrm{term}:\:\:\:\:\:\mathrm{1}.\mathrm{2}.\mathrm{3}\:\:+\:\:\mathrm{4}.\mathrm{5}.\mathrm{6}\:\:+\:\:\mathrm{7}.\mathrm{8}.\mathrm{9}\:\:+\:\:… \\ $$

Answered by Olaf_Thorendsen last updated on 24/Jul/21

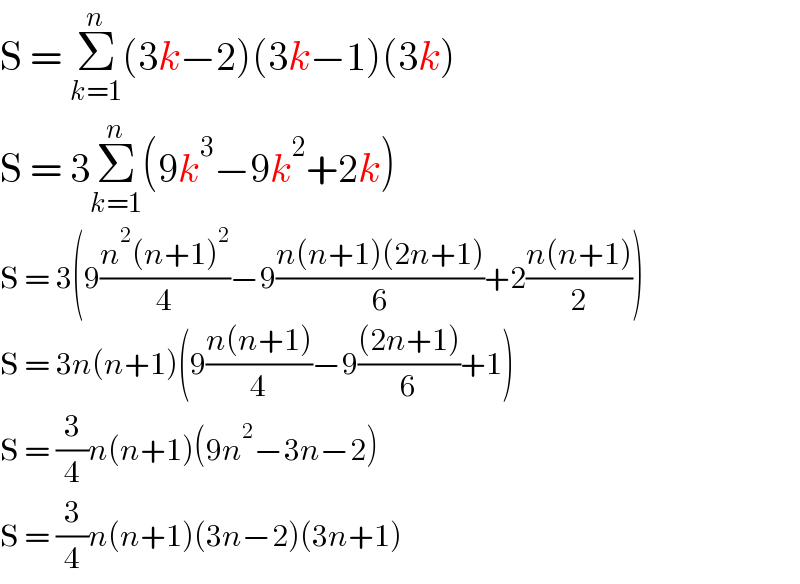
S = Σ_(k=1) ^n (3k−2)(3k−1)(3k) S = 3Σ_(k=1) ^n (9k^3 −9k^2 +2k) S = 3(9((n^2 (n+1)^2 )/4)−9((n(n+1)(2n+1))/6)+2((n(n+1))/2)) S = 3n(n+1)(9((n(n+1))/4)−9(((2n+1))/6)+1) S = (3/4)n(n+1)(9n^2 −3n−2) S = (3/4)n(n+1)(3n−2)(3n+1)

$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{3}{k}−\mathrm{2}\right)\left(\mathrm{3}{k}−\mathrm{1}\right)\left(\mathrm{3}{k}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{3}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{9}{k}^{\mathrm{3}} −\mathrm{9}{k}^{\mathrm{2}} +\mathrm{2}{k}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{3}\left(\mathrm{9}\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}−\mathrm{9}\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}+\mathrm{2}\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{3}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{9}\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{4}}−\mathrm{9}\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}+\mathrm{1}\right) \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{3}}{\mathrm{4}}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{9}{n}^{\mathrm{2}} −\mathrm{3}{n}−\mathrm{2}\right) \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{3}}{\mathrm{4}}{n}\left({n}+\mathrm{1}\right)\left(\mathrm{3}{n}−\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{1}\right) \\ $$

Commented by puissant last updated on 24/Jul/21

monsieur au debut c′est k qui varie mais vous avez mis n.. on va supposer que c′est une erreur..

$$\mathrm{monsieur}\:\mathrm{au}\:\mathrm{debut}\:\mathrm{c}'\mathrm{est}\:\mathrm{k}\:\mathrm{qui}\:\mathrm{varie}\: \\ $$$$\mathrm{mais}\:\mathrm{vous}\:\mathrm{avez}\:\mathrm{mis}\:\mathrm{n}..\:\mathrm{on}\:\mathrm{va}\:\mathrm{supposer} \\ $$$$\mathrm{que}\:\mathrm{c}'\mathrm{est}\:\mathrm{une}\:\mathrm{erreur}.. \\ $$

Commented by Tawa11 last updated on 24/Jul/21

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciste}. \\ $$

Commented by Olaf_Thorendsen last updated on 24/Jul/21

$$\mathrm{bien}\:\mathrm{vu}. \\ $$

Facebook Tweet Pin

Find-the-sum-to-n-term-1-2-3-4-5-6-7-8-9-

Leave a Reply Cancel reply