Question Number 121472 by ATHISHHUZAIN last updated on 08/Nov/20
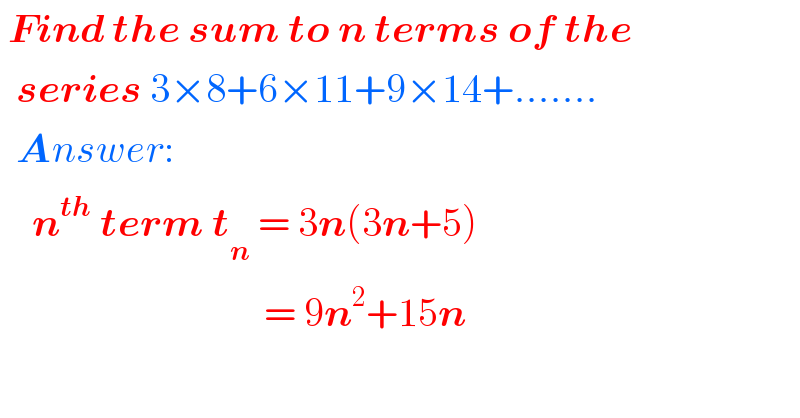
$$\:\boldsymbol{{Find}}\:\boldsymbol{{the}}\:\boldsymbol{{sum}}\:\boldsymbol{{to}}\:\boldsymbol{{n}}\:\boldsymbol{{terms}}\:\boldsymbol{{of}}\:\boldsymbol{{the}} \\ $$$$\:\:\boldsymbol{{series}}\:\mathrm{3}×\mathrm{8}+\mathrm{6}×\mathrm{11}+\mathrm{9}×\mathrm{14}+……. \\ $$$$\:\:\boldsymbol{{A}}{nswer}: \\ $$$$\:\:\:\:\boldsymbol{{n}}^{\boldsymbol{{th}}} \:\boldsymbol{{term}}\:\boldsymbol{{t}}_{\boldsymbol{{n}}} \:=\:\mathrm{3}\boldsymbol{{n}}\left(\mathrm{3}\boldsymbol{{n}}+\mathrm{5}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{9}\boldsymbol{{n}}^{\mathrm{2}} +\mathrm{15}\boldsymbol{{n}} \\ $$$$\:\:\:\:\:\: \\ $$
Answered by TANMAY PANACEA last updated on 08/Nov/20
![T_n =3n[8+(n−1)3]=3n(3n+5)=9n^2 +15n S_n =Σ_(n=1) ^n T_n =9Σ_(n=1) ^n n^2 +15Σ_(n=1) ^n n S_n =9×((n(n+1)(2n+1))/6)+15×((n(n+1))/2)](https://www.tinkutara.com/question/Q121482.png)
$${T}_{{n}} =\mathrm{3}{n}\left[\mathrm{8}+\left({n}−\mathrm{1}\right)\mathrm{3}\right]=\mathrm{3}{n}\left(\mathrm{3}{n}+\mathrm{5}\right)=\mathrm{9}{n}^{\mathrm{2}} +\mathrm{15}{n} \\ $$$${S}_{{n}} =\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{T}_{{n}} =\mathrm{9}\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{n}^{\mathrm{2}} +\mathrm{15}\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{n} \\ $$$${S}_{{n}} =\mathrm{9}×\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}+\mathrm{15}×\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$ \\ $$
