Question Number 98988 by Rio Michael last updated on 17/Jun/20
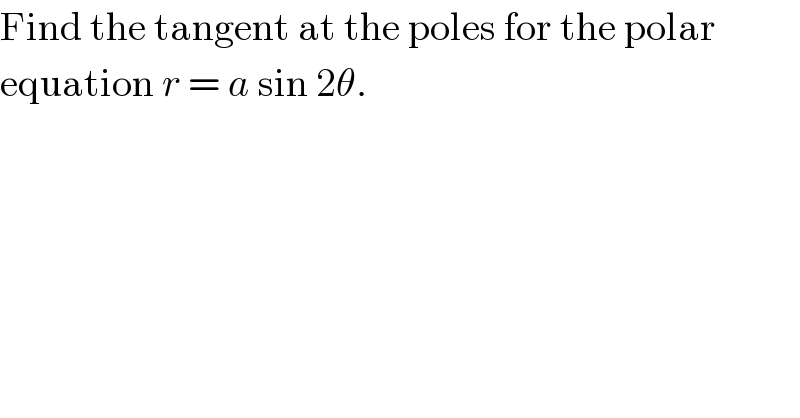
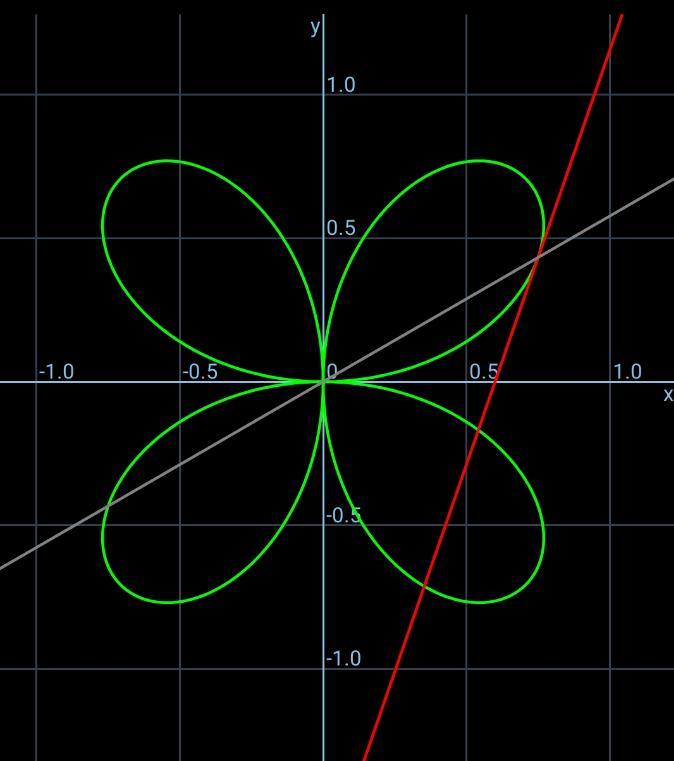
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{at}\:\mathrm{the}\:\mathrm{poles}\:\mathrm{for}\:\mathrm{the}\:\mathrm{polar} \\ $$$$\mathrm{equation}\:{r}\:=\:{a}\:\mathrm{sin}\:\mathrm{2}\theta. \\ $$
Answered by mr W last updated on 17/Jun/20
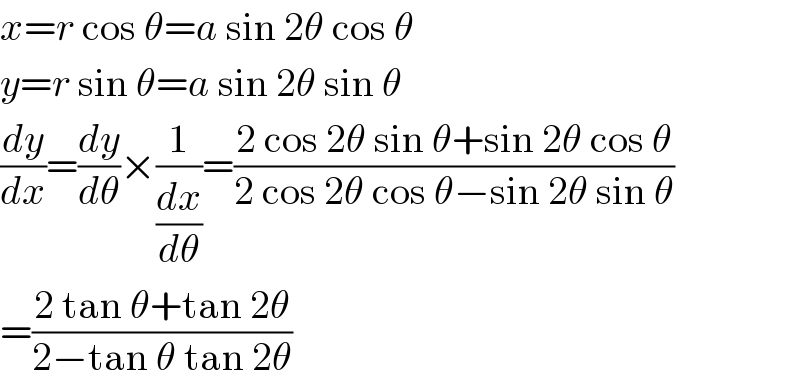
$${x}={r}\:\mathrm{cos}\:\theta={a}\:\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{cos}\:\theta \\ $$$${y}={r}\:\mathrm{sin}\:\theta={a}\:\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{sin}\:\theta \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{d}\theta}×\frac{\mathrm{1}}{\frac{{dx}}{{d}\theta}}=\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta\:\mathrm{sin}\:\theta+\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{cos}\:\theta}{\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta\:\mathrm{cos}\:\theta−\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{sin}\:\theta} \\ $$$$=\frac{\mathrm{2}\:\mathrm{tan}\:\theta+\mathrm{tan}\:\mathrm{2}\theta}{\mathrm{2}−\mathrm{tan}\:\theta\:\mathrm{tan}\:\mathrm{2}\theta} \\ $$
Commented by Rio Michael last updated on 17/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 17/Jun/20