Question Number 170297 by ali009 last updated on 19/May/22
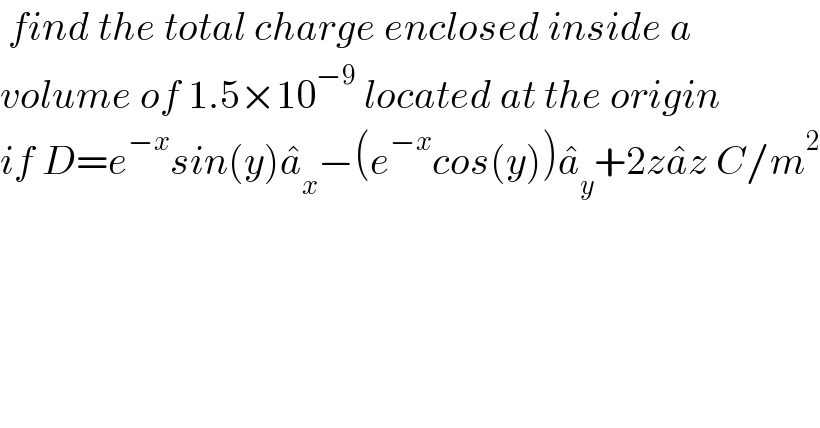
$$\:{find}\:{the}\:{total}\:{charge}\:{enclosed}\:{inside}\:{a}\: \\ $$$${volume}\:{of}\:\mathrm{1}.\mathrm{5}×\mathrm{10}^{−\mathrm{9}} \:{located}\:{at}\:{the}\:{origin} \\ $$$${if}\:{D}={e}^{−{x}} {sin}\left({y}\right)\hat {{a}}_{{x}} −\left({e}^{−{x}} {cos}\left({y}\right)\right)\hat {{a}}_{{y}} +\mathrm{2}{z}\hat {{a}z}\:{C}/{m}^{\mathrm{2}} \\ $$
Answered by ali009 last updated on 20/May/22
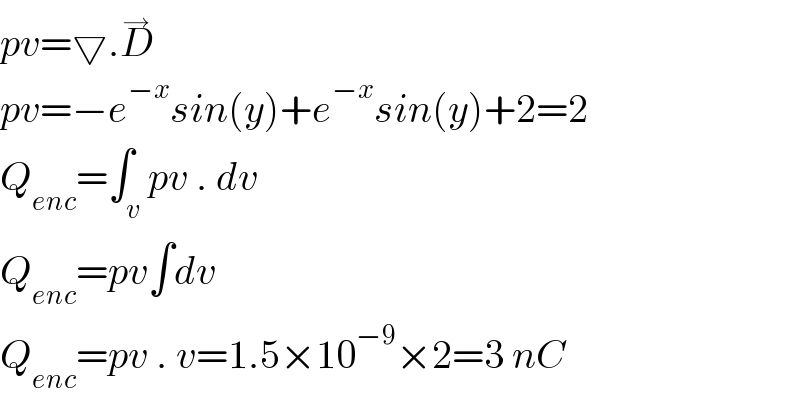
$${pv}=\bigtriangledown.\overset{\rightarrow} {{D}} \\ $$$${pv}=−{e}^{−{x}} {sin}\left({y}\right)+{e}^{−{x}} {sin}\left({y}\right)+\mathrm{2}=\mathrm{2} \\ $$$${Q}_{{enc}} =\int_{{v}} {pv}\:.\:{dv} \\ $$$${Q}_{{enc}} ={pv}\int{dv} \\ $$$${Q}_{{enc}} ={pv}\:.\:{v}=\mathrm{1}.\mathrm{5}×\mathrm{10}^{−\mathrm{9}} ×\mathrm{2}=\mathrm{3}\:{nC} \\ $$
