Question Number 117369 by bemath last updated on 11/Oct/20
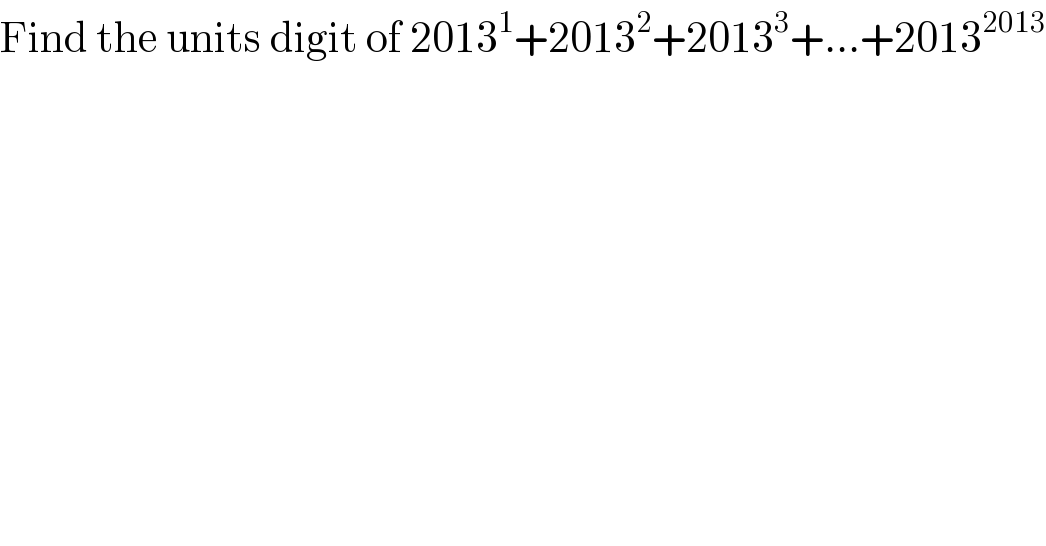
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{units}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{2013}^{\mathrm{1}} +\mathrm{2013}^{\mathrm{2}} +\mathrm{2013}^{\mathrm{3}} +…+\mathrm{2013}^{\mathrm{2013}} \\ $$
Answered by JDamian last updated on 11/Oct/20

$${S}=\mathrm{2013}^{\mathrm{1}} +\mathrm{2013}^{\mathrm{2}} +\:\centerdot\centerdot\centerdot\:+\:\mathrm{2013}^{\mathrm{2013}} \\ $$$${S}\:{mod}\:\mathrm{10}\:=\:\left(\mathrm{3}^{\mathrm{1}} +\mathrm{3}^{\mathrm{2}} +\centerdot\centerdot\centerdot+\mathrm{3}^{\mathrm{2013}} \right){mod}\:\mathrm{10} \\ $$$$\mathrm{The}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{these}\:\mathrm{powers}\:\mathrm{are} \\ $$$$\mathrm{3},\:\mathrm{9},\:\mathrm{7},\:\mathrm{1},\:\mathrm{3},\:\mathrm{9},\:\mathrm{7},\:\mathrm{1},\:\centerdot\centerdot\centerdot \\ $$$$\mathrm{And}\:\mathrm{the}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\mathrm{3},\:\mathrm{2},\:\mathrm{9},\:\mathrm{0},\:\mathrm{3},\:\mathrm{2},\:\mathrm{9},\:\mathrm{0},\:\centerdot\centerdot\centerdot \\ $$$$\mathrm{As}\:\:\:\mathrm{2013}\:\equiv\:\mathrm{1}\:{mod}\:\mathrm{4}\:\:\:\:{the}\:{answer}\:{is}\:\mathrm{3} \\ $$
