Question Number 144929 by gsk2684 last updated on 30/Jun/21
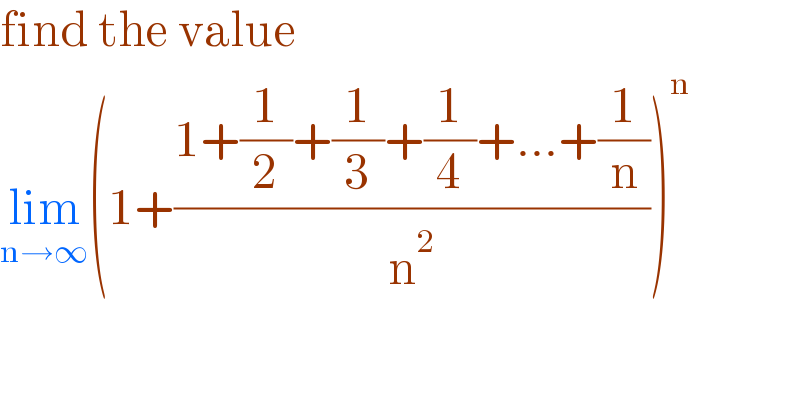
$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\: \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{\mathrm{n}}}{\mathrm{n}^{\mathrm{2}} }\right)^{\mathrm{n}} \:\: \\ $$
Answered by mathmax by abdo last updated on 30/Jun/21
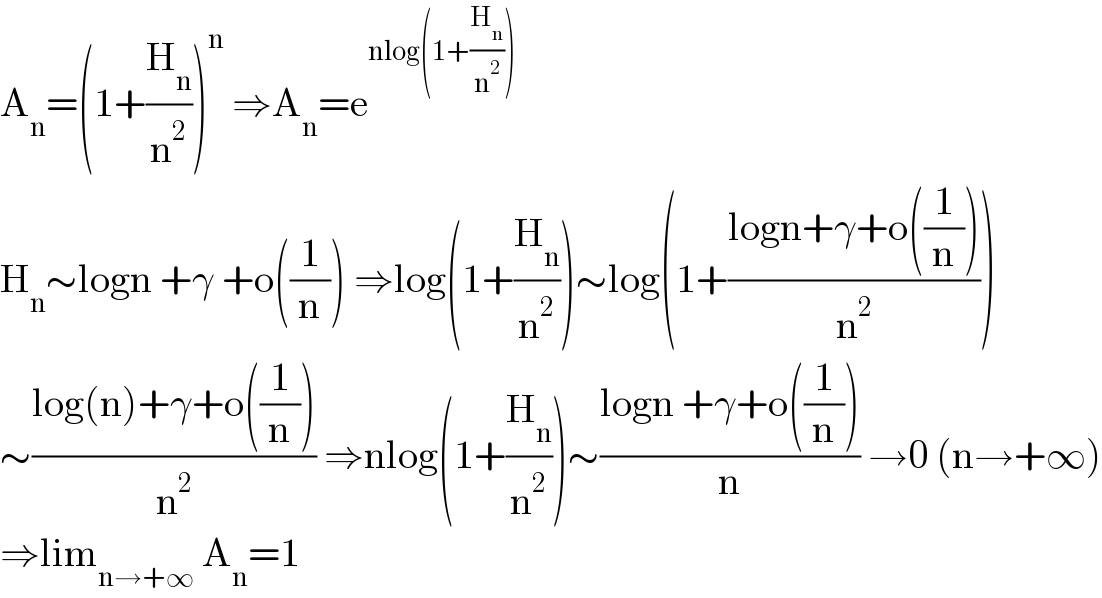
$$\mathrm{A}_{\mathrm{n}} =\left(\mathrm{1}+\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\right)^{\mathrm{n}} \:\Rightarrow\mathrm{A}_{\mathrm{n}} =\mathrm{e}^{\mathrm{nlog}\left(\mathrm{1}+\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\right)} \\ $$$$\mathrm{H}_{\mathrm{n}} \sim\mathrm{logn}\:+\gamma\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\:\Rightarrow\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\right)\sim\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{logn}+\gamma+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{n}^{\mathrm{2}} }\right) \\ $$$$\sim\frac{\mathrm{log}\left(\mathrm{n}\right)+\gamma+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{n}^{\mathrm{2}} }\:\Rightarrow\mathrm{nlog}\left(\mathrm{1}+\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\right)\sim\frac{\mathrm{logn}\:+\gamma+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{n}}\:\rightarrow\mathrm{0}\:\left(\mathrm{n}\rightarrow+\infty\right) \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{1} \\ $$
Commented by gsk2684 last updated on 30/Jun/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathmax by abdo last updated on 30/Jun/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
