Question Number 39386 by maxmathsup by imad last updated on 05/Jul/18
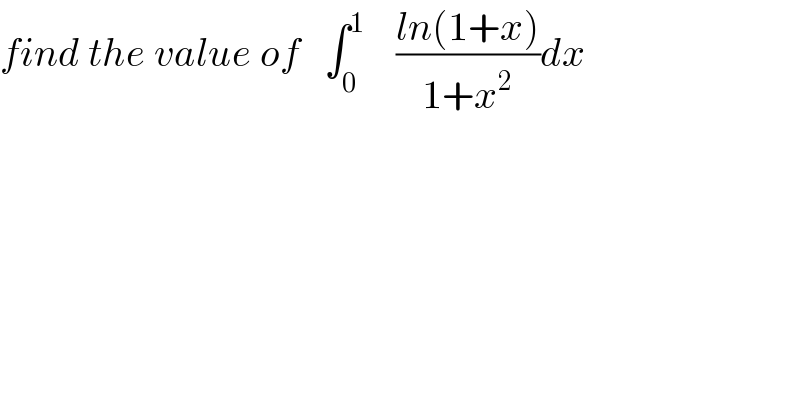
$${find}\:{the}\:{value}\:{of}\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$
Commented by abdo mathsup 649 cc last updated on 08/Jul/18
![let I = ∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx changement x=tant give I = ∫_0 ^(π/4) ((ln(1+tant))/(1+tan^2 t)) (1+tan^2 t)dt = ∫_0 ^(π/4) ln (1+tant)dt let consider f(x) =∫_0 ^(π/4) ln(1+xtant)dt we have f^′ (x) = ∫_0 ^(π/4) ((tant)/(1+xtant)) dt = ∫_0 ^(π/4) ((sint)/(cost(1+x ((sint)/(cost)))))dt = ∫_0 ^(π/4) ((sint)/(cost +x sint)) dt chsngement tan((t/2))=u give f(x) = ∫_0 ^((√2) −1) (((2u)/(1+u^2 ))/(((1−u^2 )/(1+u^2 )) +x ((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) = ∫_0 ^((√2) −1) ((4u)/((1+u^2 )( 1−u^2 +2xu)))du =− ∫_0 ^((√2) −1) ((4u)/((u^2 +1)(u^2 −2xu −1)))du let decompose F(u)= ((4u)/((u^2 +1)(u^2 −2xu −1))) roots of u^2 −2xu −1 Δ^′ =x^(2 ) +1 ⇒ u_1 =x+(√(1+x^2 )) u_2 =x−(√(1+x^2 )) F(u) = ((4u)/((u^2 +1)(u−u_1 )(u −u_2 ))) = (a/(u −u_1 )) +(b/(u−u_2 )) +((cu +d)/(u^2 +1)) a = ((4u_1 )/((u_1 ^2 +1)(u_1 −u_2 ))) b = ((4u_2 )/((u_2 ^2 +1)(u_2 −u_1 ))) lim_(u→+∞) u F(u)=0 = a+b +c ⇒ c =−a−b ⇒ F(u) = (a/(u−u_1 )) +(b/(u−u_2 )) +(((−a−b)u +d)/(u^2 +1)) F(0) =0 = −(a/u_1 ) −(b/u_2 ) +d ⇒d = (a/u_1 ) +(b/u_2 ) ⇒ F(u) = (a/(u−u_1 )) +(b/(u−u_2 )) +(((−a−b)u +(a/u_1 ) +(b/u_2 ))/(u^2 +1)) ∫ F(u)du =a ln∣u−u_1 ∣ +b ln∣u−u_2 ∣ −((a+b)/2) ln(u^2 +1) +((a/u_1 ) +(b/u_2 )) arctanu +k and ∫_0 ^((√2) −1) F(u)du =[aln∣u−u_1 ∣ +bln∣u−u_2 ∣ −((a+b)/2)ln(1+u^2 ) + ((au_2 +bu_1 )/(u_1 u_2 )) arctan(u)]_0 ^((√2)−1) =a ln∣(√2)−1 −u_1 ∣ +bln∣(√2)−1−u_2 ∣ −((a+b)/2) ln(1+((√2) −1)^2 ) +((au_2 +bu_1 )/(u_1 u_2 )) arctan((√2)−1) −a ln∣u_1 ∣−b ln∣u_2 ∣ and f(x) =−∫_0 ^((√2) −1) F(u)du ...be continued...](https://www.tinkutara.com/question/Q39630.png)
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:{changement}\:{x}={tant} \\ $$$${give}\: \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{ln}\left(\mathrm{1}+{tant}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} {t}}\:\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\:\left(\mathrm{1}+{tant}\right){dt}\:{let}\:{consider} \\ $$$${f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left(\mathrm{1}+{xtant}\right){dt}\:{we}\:{have} \\ $$$${f}^{'} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{tant}}{\mathrm{1}+{xtant}}\:{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\frac{{sint}}{{cost}\left(\mathrm{1}+{x}\:\frac{{sint}}{{cost}}\right)}{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\frac{{sint}}{{cost}\:+{x}\:{sint}}\:{dt}\:\:{chsngement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u} \\ $$$${give} \\ $$$${f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\frac{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\:+{x}\:\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\:\:\:\:\frac{\mathrm{4}{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\:\mathrm{1}−{u}^{\mathrm{2}} \:+\mathrm{2}{xu}\right)}{du} \\ $$$$=−\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{4}{u}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:−\mathrm{2}{xu}\:−\mathrm{1}\right)}{du} \\ $$$${let}\:{decompose}\:{F}\left({u}\right)=\:\frac{\mathrm{4}{u}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:−\mathrm{2}{xu}\:−\mathrm{1}\right)} \\ $$$${roots}\:{of}\:{u}^{\mathrm{2}} \:−\mathrm{2}{xu}\:−\mathrm{1} \\ $$$$\Delta^{'} \:={x}^{\mathrm{2}\:} \:+\mathrm{1}\:\Rightarrow\:{u}_{\mathrm{1}} ={x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${u}_{\mathrm{2}} ={x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${F}\left({u}\right)\:=\:\frac{\mathrm{4}{u}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}−{u}_{\mathrm{1}} \right)\left({u}\:−{u}_{\mathrm{2}} \right)} \\ $$$$=\:\frac{{a}}{{u}\:−{u}_{\mathrm{1}} }\:\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:=\:\frac{\mathrm{4}{u}_{\mathrm{1}} }{\left({u}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}_{\mathrm{1}} \:−{u}_{\mathrm{2}} \right)} \\ $$$${b}\:=\:\frac{\mathrm{4}{u}_{\mathrm{2}} }{\left({u}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}_{\mathrm{2}} \:−{u}_{\mathrm{1}} \right)} \\ $$$${lim}_{{u}\rightarrow+\infty} {u}\:{F}\left({u}\right)=\mathrm{0}\:=\:{a}+{b}\:\:+{c}\:\Rightarrow \\ $$$${c}\:=−{a}−{b}\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\:\:\frac{{a}}{{u}−{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{\left(−{a}−{b}\right){u}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=\:−\frac{{a}}{{u}_{\mathrm{1}} }\:−\frac{{b}}{{u}_{\mathrm{2}} }\:+{d}\:\Rightarrow{d}\:=\:\frac{{a}}{{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}_{\mathrm{2}} }\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\:\frac{{a}}{{u}−{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}−{u}_{\mathrm{2}} }\:+\frac{\left(−{a}−{b}\right){u}\:+\frac{{a}}{{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}_{\mathrm{2}} }}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\int\:{F}\left({u}\right){du}\:={a}\:{ln}\mid{u}−{u}_{\mathrm{1}} \mid\:+{b}\:{ln}\mid{u}−{u}_{\mathrm{2}} \mid \\ $$$$−\frac{{a}+{b}}{\mathrm{2}}\:{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\:\:+\left(\frac{{a}}{{u}_{\mathrm{1}} }\:+\frac{{b}}{{u}_{\mathrm{2}} }\right)\:{arctanu}\:+{k}\:{and} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:{F}\left({u}\right){du}\:\:=\left[{aln}\mid{u}−{u}_{\mathrm{1}} \mid\:+{bln}\mid{u}−{u}_{\mathrm{2}} \mid\right. \\ $$$$\left.−\frac{{a}+{b}}{\mathrm{2}}{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\:+\:\frac{{au}_{\mathrm{2}} \:+{bu}_{\mathrm{1}} }{{u}_{\mathrm{1}} {u}_{\mathrm{2}} }\:{arctan}\left({u}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$={a}\:{ln}\mid\sqrt{\mathrm{2}}−\mathrm{1}\:−{u}_{\mathrm{1}} \mid\:+{bln}\mid\sqrt{\mathrm{2}}−\mathrm{1}−{u}_{\mathrm{2}} \mid \\ $$$$−\frac{{a}+{b}}{\mathrm{2}}\:{ln}\left(\mathrm{1}+\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)^{\mathrm{2}} \right)\:\:+\frac{{au}_{\mathrm{2}} \:+{bu}_{\mathrm{1}} }{{u}_{\mathrm{1}} {u}_{\mathrm{2}} }\:{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$−{a}\:{ln}\mid{u}_{\mathrm{1}} \mid−{b}\:{ln}\mid{u}_{\mathrm{2}} \mid\:{and}\: \\ $$$${f}\left({x}\right)\:=−\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:{F}\left({u}\right){du}\:…{be}\:{continued}… \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jul/18
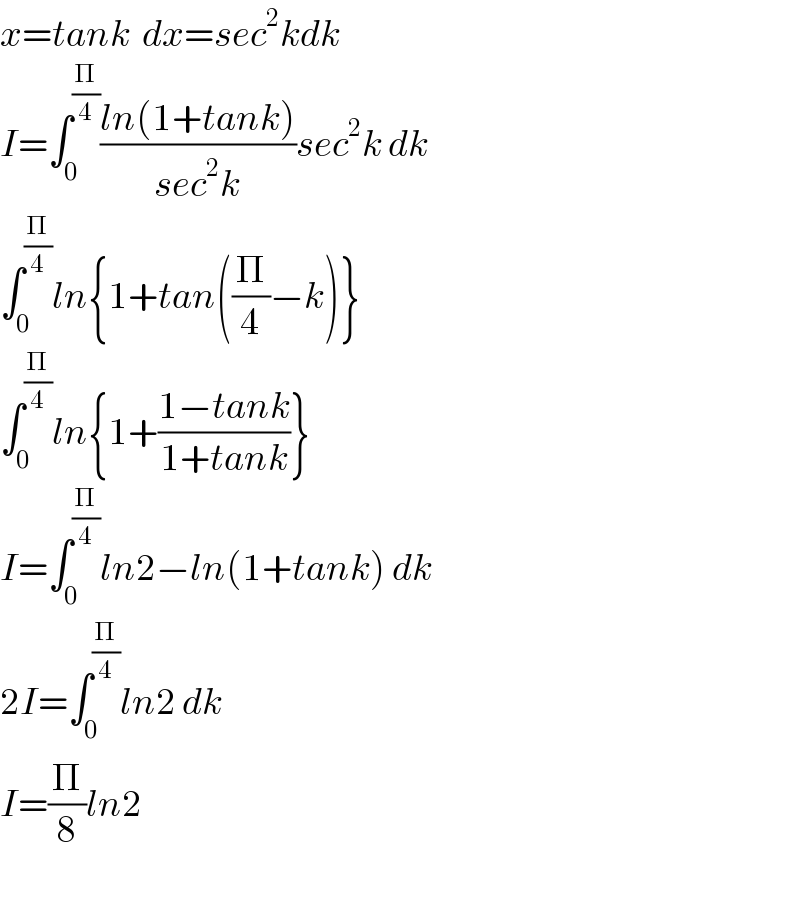
$${x}={tank}\:\:{dx}={sec}^{\mathrm{2}} {kdk} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{ln}\left(\mathrm{1}+{tank}\right)}{{sec}^{\mathrm{2}} {k}}{sec}^{\mathrm{2}} {k}\:{dk} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\left\{\mathrm{1}+{tan}\left(\frac{\Pi}{\mathrm{4}}−{k}\right)\right\} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\left\{\mathrm{1}+\frac{\mathrm{1}−{tank}}{\mathrm{1}+{tank}}\right\} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\mathrm{2}−{ln}\left(\mathrm{1}+{tank}\right)\:{dk} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\mathrm{2}\:{dk} \\ $$$${I}=\frac{\Pi}{\mathrm{8}}{ln}\mathrm{2} \\ $$$$ \\ $$
