Question Number 40154 by maxmathsup by imad last updated on 16/Jul/18
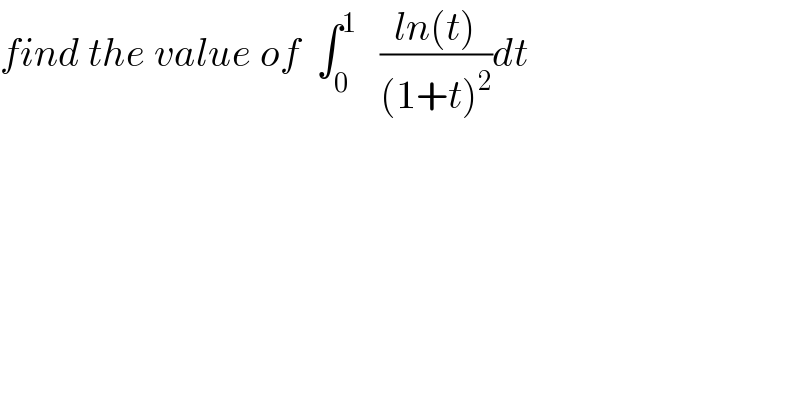
$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$
Commented by maxmathsup by imad last updated on 16/Jul/18
![let I = ∫_0 ^1 ((ln(t))/((1+t)^2 ))dt let integrate by parts u^′ =(1/((1+t)^2 )) and v=ln(t) I = [(1−(1/(1+t)))ln(t)]_0 ^1 −∫_0 ^1 (1−(1/(1+t)))(dt/t) = −∫_0 ^1 (dt/(1+t)) =−[ln∣1+t∣]_0 ^1 =−ln(2) I =−ln(2) .](https://www.tinkutara.com/question/Q40201.png)
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}\:\:\:{let}\:{integrate}\:{by}\:{parts}\:{u}^{'} =\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\:\:{and}\:{v}={ln}\left({t}\right) \\ $$$${I}\:=\:\left[\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){ln}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right)\frac{{dt}}{{t}} \\ $$$$=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{1}+{t}}\:\:=−\left[{ln}\mid\mathrm{1}+{t}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:=−{ln}\left(\mathrm{2}\right) \\ $$$${I}\:=−{ln}\left(\mathrm{2}\right)\:. \\ $$
Answered by ajfour last updated on 16/Jul/18
![I=∫_0 ^( 1) ((ln t)/((1+t)^2 )) = −((ln t)/((1+t)))∣_0 ^1 +∫_0 ^( 1) (dt/(t(1+t))) = lim_(t→0) [(((ln t)/(1+t)))−ln ((t/(1+t)))]−ln 2 =lim_(t→0) [ln (((1+t)t^(1+t) )/t)]−ln 2 =lim_(t→0) [ln (1+t)t^t ]−ln 2 =lim_(t→0) ln (1+t)+lim_(t→0) ((ln t)/((1/t)))−ln 2 = 0+lim_(t→0) (((1/t)/(−1/t^2 ))) −ln 2 I= −ln 2 .](https://www.tinkutara.com/question/Q40169.png)
$${I}=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\mathrm{ln}\:{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\: \\ $$$$\:\:=\:−\frac{\mathrm{ln}\:{t}}{\left(\mathrm{1}+{t}\right)}\mid_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{dt}}{{t}\left(\mathrm{1}+{t}\right)} \\ $$$$\:\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\frac{\mathrm{ln}\:{t}}{\mathrm{1}+{t}}\right)−\mathrm{ln}\:\left(\frac{{t}}{\mathrm{1}+{t}}\right)\right]−\mathrm{ln}\:\mathrm{2} \\ $$$$\:\:=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\mathrm{ln}\:\frac{\left(\mathrm{1}+{t}\right){t}^{\mathrm{1}+{t}} }{{t}}\right]−\mathrm{ln}\:\mathrm{2} \\ $$$$\:\:=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\mathrm{ln}\:\left(\mathrm{1}+{t}\right){t}^{{t}} \right]−\mathrm{ln}\:\mathrm{2} \\ $$$$\:\:=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}ln}\:\left(\mathrm{1}+{t}\right)+\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:{t}}{\left(\mathrm{1}/{t}\right)}−\mathrm{ln}\:\mathrm{2} \\ $$$$\:\:=\:\mathrm{0}+\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}/{t}}{−\mathrm{1}/{t}^{\mathrm{2}} }\right)\:−\mathrm{ln}\:\mathrm{2} \\ $$$$\:{I}=\:−\mathrm{ln}\:\mathrm{2}\:. \\ $$$$ \\ $$
