Question Number 34228 by abdo imad last updated on 03/May/18
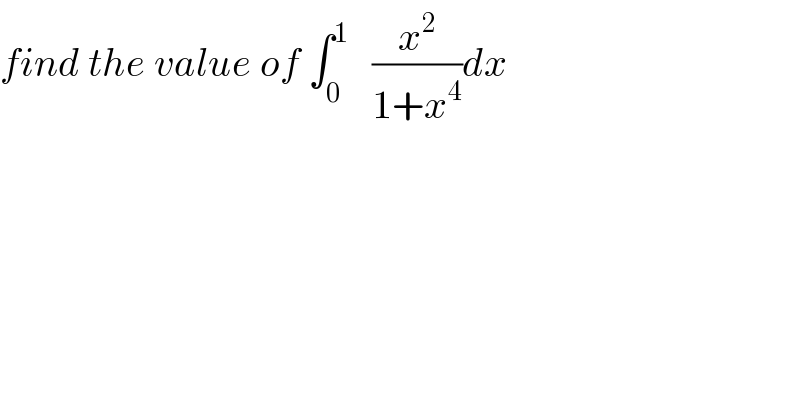
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}} }{dx} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/May/18
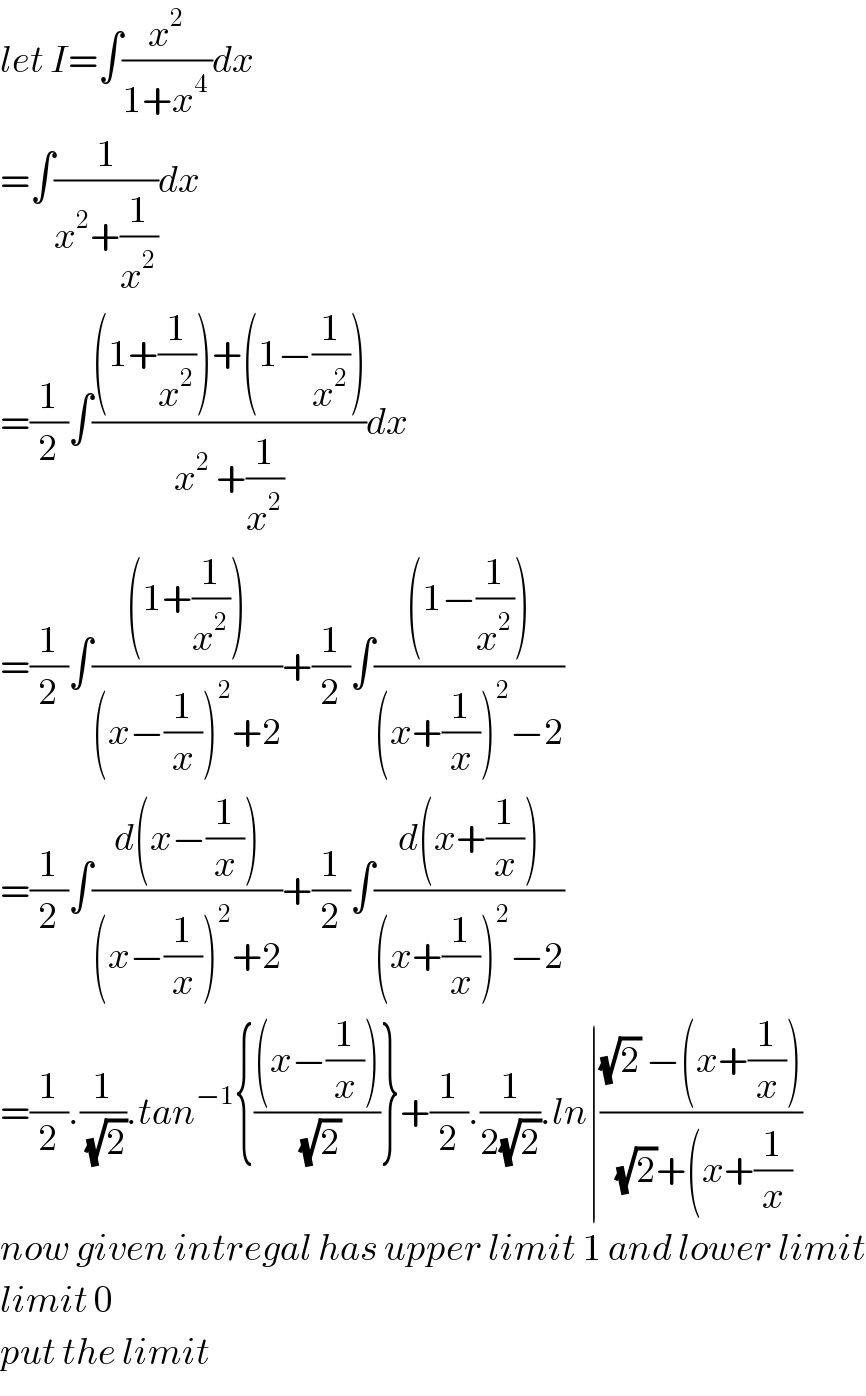
$${let}\:{I}=\int\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}\:} }{dx} \\ $$$$=\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}.{tan}^{−\mathrm{1}} \left\{\frac{\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\:\sqrt{\mathrm{2}}}\right\}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}.{ln}\mid\frac{\sqrt{\mathrm{2}}\:−\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\:\sqrt{\mathrm{2}}+\left({x}+\frac{\mathrm{1}}{{x}}\right.} \\ $$$${now}\:{given}\:{intregal}\:{has}\:{upper}\:{limit}\:\mathrm{1}\:{and}\:{lower}\:{limit} \\ $$$${limit}\:\mathrm{0} \\ $$$${put}\:{the}\:{limit} \\ $$
