Question Number 34561 by math khazana by abdo last updated on 08/May/18
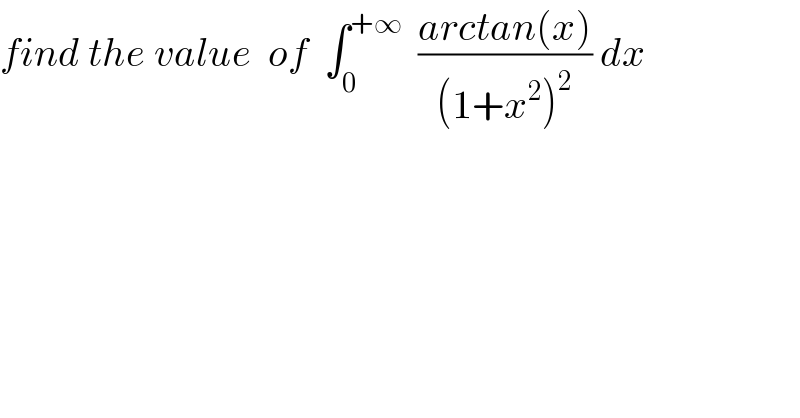
$${find}\:{the}\:{value}\:\:{of}\:\:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{{arctan}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx} \\ $$
Commented by math khazana by abdo last updated on 09/May/18
![∫_0 ^∞ ((arctanx)/((1+x^2 )^2 ))dx = [(1/(4 )) (arctanx)^2 +(1/4) sin(2arctanx)]_0 ^(+∞) = (1/4)( (π/2))^2 +0 = (π^2 /(16)) .](https://www.tinkutara.com/question/Q34619.png)
$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctanx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:=\:\left[\frac{\mathrm{1}}{\mathrm{4}\:}\:\left({arctanx}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4}}\:{sin}\left(\mathrm{2}{arctanx}\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\:\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} \:+\mathrm{0}\:\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\:\:. \\ $$
