Menu Close

find-the-value-of-0-arctan-x-1-x-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 52418 by Abdo msup. last updated on 07/Jan/19
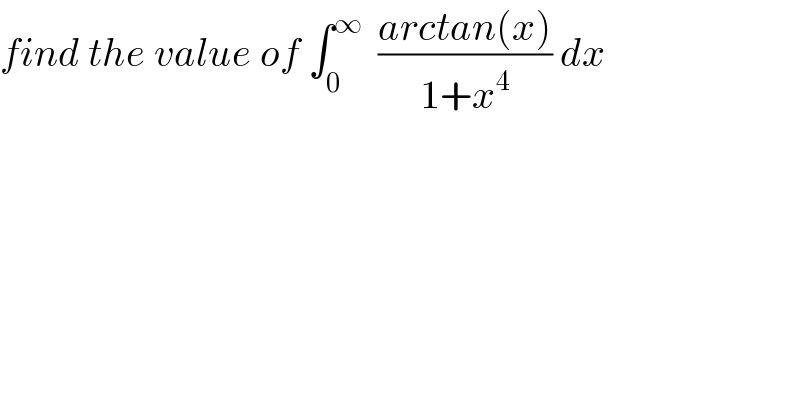
find the value of ∫_0 ^∞ ((arctan(x))/(1+x^4 )) dx
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx} \\ $$
Commented by maxmathsup by imad last updated on 08/Jan/19
let f(t)=∫_0 ^∞ ((arctan(tx))/(1+x^4 ))dx ⇒f^′ (t)=∫_0 ^∞ (x/((1+x^2 t^2 )(1+x^4 )))dx =_(xt=u) ∫_0 ^∞ (u/(t(1+u^2 )(1+(u^4 /t^4 )))) (du/t) =∫_0 ^∞ (u/((1+u^2 )(t^2 +(u^4 /t^2 ))))du =t^2 ∫_0 ^∞ (u/((u^2 +1)(u^4 +t^4 )))du let decompose F(u)=(u/((u^2 +1)(u^4 +t^4 ))) F(u) =(u/((u^2 +1)((u^2 +t^2 )^2 −2u^2 t^2 ))) =(u/((u^2 +1)(u^2 +t^2 −(√2)tu)(u^2 +t^2 +(√2)tu))) =((au +b)/(u^2 +1)) +((cu+d)/(u^2 −(√2)tu +t^2 )) +((eu +f)/(u^2 +(√2)tu +t^2 )) F(−u)=−F(u)⇒((−au+b)/(u^2 +1)) +((−cu+d)/(u^2 +(√2)tu +t^2 )) +((−eu +f)/(u^2 −(√2)tu +t^2 )) =((−au−b)/(u^2 +1)) +((−cu−d)/(u^2 −(√2)tu +t^2 )) +((−eu −f)/(u^2 +(√2)tu +t^2 )) ⇒ b=0 and c=e and f=−d ⇒ F(u)=((au)/(u^2 +1)) +((cu+d)/(u^2 −(√2)tu +t^2 )) +((cu−d)/(u^2 +(√2)tu +t^2 )) lim_(u→+∞) uF(u)=0 =a +2c ⇒c=−(a/2) ⇒ F(u)=((au)/(u^2 +1)) −(1/2) ((au−2d)/(u^2 −(√2)tu +t^2 )) −(1/2) ((au+2d)/(u^2 +(√2)tu +t^2 )) F(1) =(1/(2(1+t^4 ))) =(a/2) −(1/2) ((a−2d)/(1+t^2 −(√2)t)) −(1/2) ((a+2d)/(1+t^2 +(√2)t)) F(−1) =((−1)/(2(1+t^4 ))) −(1/2) ((a−2d)/(1+t^2 +(√2)t)) −(1/2) ((−a+2d)/(1+t^2 −(√2)t)) ....be continued...
$${let}\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({tx}\right)}{\mathrm{1}+{x}^{\mathrm{4}} }{dx}\:\:\Rightarrow{f}^{'} \left({t}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}{dx} \\ $$$$=_{{xt}={u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{u}}{{t}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{{u}^{\mathrm{4}} }{{t}^{\mathrm{4}} }\right)}\:\frac{{du}}{{t}}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} \:+\frac{{u}^{\mathrm{4}} }{{t}^{\mathrm{2}} }\right)}{du} \\ $$$$={t}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{u}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)\left({u}^{\mathrm{4}} +{t}^{\mathrm{4}} \right)}{du}\:\:\:{let}\:{decompose}\:{F}\left({u}\right)=\frac{{u}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{4}} \:+{t}^{\mathrm{4}} \right)} \\ $$$${F}\left({u}\right)\:=\frac{{u}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\left({u}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{u}^{\mathrm{2}} {t}^{\mathrm{2}} \right)}\:=\frac{{u}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} +{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{tu}\right)\left({u}^{\mathrm{2}} \:+{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{tu}\right)} \\ $$$$=\frac{{au}\:+{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{cu}+{d}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} }\:+\frac{{eu}\:+{f}}{{u}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} } \\ $$$${F}\left(−{u}\right)=−{F}\left({u}\right)\Rightarrow\frac{−{au}+{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−{cu}+{d}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} }\:+\frac{−{eu}\:+{f}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} } \\ $$$$=\frac{−{au}−{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−{cu}−{d}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} }\:+\frac{−{eu}\:−{f}}{{u}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$${b}=\mathrm{0}\:{and}\:\:{c}={e}\:\:\:{and}\:{f}=−{d}\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{{au}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{cu}+{d}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} }\:+\frac{{cu}−{d}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} } \\ $$$${lim}_{{u}\rightarrow+\infty} {uF}\left({u}\right)=\mathrm{0}\:={a}\:+\mathrm{2}{c}\:\Rightarrow{c}=−\frac{{a}}{\mathrm{2}}\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{{au}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\:\frac{{au}−\mathrm{2}{d}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{au}+\mathrm{2}{d}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{tu}\:+{t}^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}\:=\frac{{a}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{a}−\mathrm{2}{d}}{\mathrm{1}+{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{a}+\mathrm{2}{d}}{\mathrm{1}+{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}} \\ $$$${F}\left(−\mathrm{1}\right)\:=\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{a}−\mathrm{2}{d}}{\mathrm{1}+{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{−{a}+\mathrm{2}{d}}{\mathrm{1}+{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}} \\ $$$$….{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *