Question Number 26360 by abdo imad last updated on 24/Dec/17
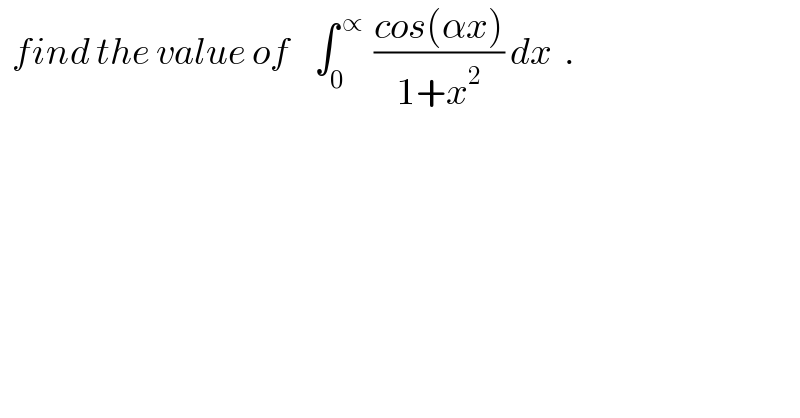
$$\:\:{find}\:{the}\:{value}\:{of}\:\:\:\:\int_{\mathrm{0}} ^{\:\propto\:} \:\frac{{cos}\left(\alpha{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:\:. \\ $$
Commented by abdo imad last updated on 25/Dec/17
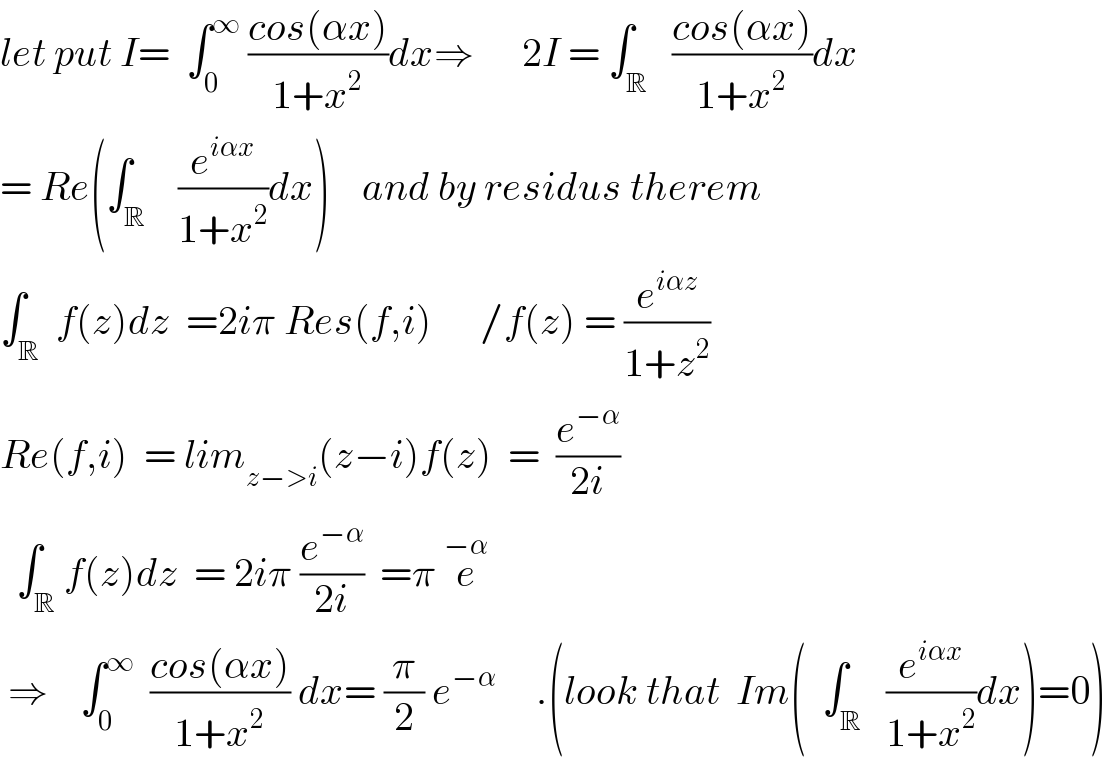
$${let}\:{put}\:{I}=\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{{cos}\left(\alpha{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\Rightarrow\:\:\:\:\:\:\mathrm{2}{I}\:=\:\int_{\mathbb{R}} \:\:\frac{{cos}\left(\alpha{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\:{Re}\left(\int_{\mathbb{R}} \:\:\:\frac{{e}^{{i}\alpha{x}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\right)\:\:\:\:{and}\:{by}\:{residus}\:{therem} \\ $$$$\int_{\mathbb{R}} \:{f}\left({z}\right){dz}\:\:=\mathrm{2}{i}\pi\:{Res}\left({f},{i}\right)\:\:\:\:\:\:/{f}\left({z}\right)\:=\:\frac{{e}^{{i}\alpha{z}} }{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$${Re}\left({f},{i}\right)\:\:=\:{lim}_{{z}−>{i}} \left({z}−{i}\right){f}\left({z}\right)\:\:=\:\:\frac{{e}^{−\alpha} }{\mathrm{2}{i}} \\ $$$$\:\:\int_{\mathbb{R}} {f}\left({z}\right){dz}\:\:=\:\mathrm{2}{i}\pi\:\frac{{e}^{−\alpha} }{\mathrm{2}{i}}\:\:=\pi\:\overset{−\alpha} {{e}} \\ $$$$\:\Rightarrow\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left(\alpha{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}=\:\frac{\pi}{\mathrm{2}}\:{e}^{−\alpha} \:\:\:\:\:.\left({look}\:{that}\:\:{Im}\left(\:\:\int_{\mathbb{R}} \:\:\frac{{e}^{{i}\alpha{x}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\right)=\mathrm{0}\right) \\ $$
