Menu Close

find-the-value-of-0-dx-1-x-2-1-x-4-

Tinku Tara 0 Comments
Pin




Question Number 33128 by prof Abdo imad last updated on 10/Apr/18
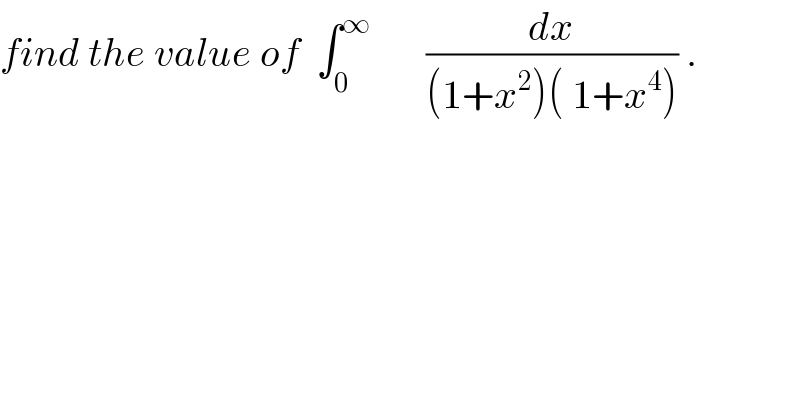
find the value of ∫_0 ^∞ (dx/((1+x^2 )( 1+x^4 ))) .
$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\:\mathrm{1}+{x}^{\mathrm{4}} \right)}\:. \\ $$
Commented by prof Abdo imad last updated on 13/Apr/18
let put I = ∫_0 ^∞ (dx/((1+x^2 )(1+x^4 ))) we have 2I = ∫_(−∞) ^(+∞) (dx/((1+x^2 )(1+x^4 ))) .let introduce the complex function ϕ(z) = (1/((1+z^2 )(1+z^4 ))) ϕ(z) = (1/((z−i)(z+i)(z^2 −i)(z^2 −(−i)))) = (1/((z−i)(z+i)(z −(√i))(z+(√i))(z −(√(−i)))(z +(√(−i))))) (√i) =e^(i(π/4)) (√(−i)) =e^(−i(π/4)) so the poles of?ϕ are i,−i,e^(i(π/4)) , −e^(i(π/4)) , e^(−i(π/4)) , −e^(−i(π/4)) ∫_(−∞) ^(+∞) ϕ(z)dz = 2iπ( Res(ϕ,i) +Res(ϕ,e^(i(π/4)) ) +Res(ϕ,−e^(−i(π/4)) ) let p(z) =(1+z^2 )(1+z^4 ) p(z)=1+z^4 +z^2 +z^6 ⇒p^′ (z) = 2z +4z^3 +6z^5 Res(ϕ,i) =(1/(p^′ (i))) = (1/(2i +4i^3 +6i^5 )) = (1/(2i−4i +6i)) = (1/(4i)) Res(ϕ, e^(i(π/4)) ) = (1/(p^′ ( e^(i(π/4)) ))) = (1/(2 e^(i(π/4)) +4 e^(i((3π)/4)) +6 e^(i((5π)/4)) )) but 2 e^(i(π/4)) +4 e^(i((3π)/4)) +6 e^(i((5π)/4)) = 2 e^(i(π/4)) −4 e^(−i(π/4)) −6 e^(i(π/4)) = −4( e^(i(π/4)) +e^(−i(π/4)) ) =−4 . 2.((√2)/2) =−4(√2) Res(ϕ,−e^(−i(π/4)) ) = (1/(p^′ ( −e^(−i(π/4)) ))) = (1/(−2 e^(−i(π/4)) −4 e^(−i((3π)/4)) −6 e^(−i((5π)/4)) )) = ((−1)/(2 e^(−i(π/4)) +4 e^(−i((3π)/4)) +6 e^(−i((5π)/4)) )) = ((−1)/(2 e^(−i(π/4)) −4 e^(i(π/4)) −6 e^(−i(π/4)) )) = ((−1)/(−4( e^(i(π/4)) +e^(−i(π/4)) ))) = (1/(4 .2.((√2)/2))) = (1/(4(√2))) ⇒ 2I =2iπ( (1/(4i)) −(1/(4(√2))) + (1/(4(√2))) ) = (π/2) ⇒ I = (π/4) .
$${let}\:{put}\:{I}\:\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}\:\:{we}\:{have} \\ $$$$\mathrm{2}{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}\:.{let}\:{introduce}\:{the} \\ $$$${complex}\:{function}\:\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\left(\mathrm{1}+{z}^{\mathrm{4}} \right)} \\ $$$$\varphi\left({z}\right)\:=\:\:\frac{\mathrm{1}}{\left({z}−{i}\right)\left({z}+{i}\right)\left({z}^{\mathrm{2}} \:−{i}\right)\left({z}^{\mathrm{2}} \:−\left(−{i}\right)\right)} \\ $$$$=\:\:\frac{\mathrm{1}}{\left({z}−{i}\right)\left({z}+{i}\right)\left({z}\:−\sqrt{{i}}\right)\left({z}+\sqrt{{i}}\right)\left({z}\:−\sqrt{−{i}}\right)\left({z}\:+\sqrt{−{i}}\right)} \\ $$$$\sqrt{{i}}\:={e}^{{i}\frac{\pi}{\mathrm{4}}} \:\:\:\:\sqrt{−{i}}\:={e}^{−{i}\frac{\pi}{\mathrm{4}}} \:\:{so}\:{the}\:{poles}\:{of}?\varphi\:{are}\: \\ $$$${i},−{i},{e}^{{i}\frac{\pi}{\mathrm{4}}} \:,\:−{e}^{{i}\frac{\pi}{\mathrm{4}}} \:,\:{e}^{−{i}\frac{\pi}{\mathrm{4}}} \:,\:−{e}^{−{i}\frac{\pi}{\mathrm{4}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\:\mathrm{2}{i}\pi\left(\:\:{Res}\left(\varphi,{i}\right)\:+{Res}\left(\varphi,{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)\:+{Res}\left(\varphi,−{e}^{−{i}\frac{\pi}{\mathrm{4}}} \right)\right. \\ $$$${let}\:{p}\left({z}\right)\:=\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\left(\mathrm{1}+{z}^{\mathrm{4}} \right) \\ $$$${p}\left({z}\right)=\mathrm{1}+{z}^{\mathrm{4}} \:\:+{z}^{\mathrm{2}} \:+{z}^{\mathrm{6}} \:\Rightarrow{p}^{'} \left({z}\right)\:=\:\mathrm{2}{z}\:\:+\mathrm{4}{z}^{\mathrm{3}} \:+\mathrm{6}{z}^{\mathrm{5}} \\ $$$${Res}\left(\varphi,{i}\right)\:=\frac{\mathrm{1}}{{p}^{'} \left({i}\right)}\:=\:\:\frac{\mathrm{1}}{\mathrm{2}{i}\:+\mathrm{4}{i}^{\mathrm{3}} \:+\mathrm{6}{i}^{\mathrm{5}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}{i}−\mathrm{4}{i}\:+\mathrm{6}{i}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}{i}} \\ $$$${Res}\left(\varphi,\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)\:\:=\:\:\frac{\mathrm{1}}{{p}^{'} \left(\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)}\:=\:\:\frac{\mathrm{1}}{\mathrm{2}\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \:\:+\mathrm{4}\:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \:\:+\mathrm{6}\:{e}^{{i}\frac{\mathrm{5}\pi}{\mathrm{4}}} } \\ $$$${but}\:\:\mathrm{2}\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \:\:+\mathrm{4}\:\:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \:\:+\mathrm{6}\:{e}^{{i}\frac{\mathrm{5}\pi}{\mathrm{4}}} \\ $$$$=\:\mathrm{2}\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \:\:−\mathrm{4}\:{e}^{−{i}\frac{\pi}{\mathrm{4}}} \:−\mathrm{6}\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \:=\:−\mathrm{4}\left(\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \:+{e}^{−{i}\frac{\pi}{\mathrm{4}}} \right) \\ $$$$=−\mathrm{4}\:.\:\mathrm{2}.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=−\mathrm{4}\sqrt{\mathrm{2}} \\ $$$${Res}\left(\varphi,−{e}^{−{i}\frac{\pi}{\mathrm{4}}} \right)\:\:=\:\frac{\mathrm{1}}{{p}^{'} \left(\:−{e}^{−{i}\frac{\pi}{\mathrm{4}}} \right)} \\ $$$$=\:\:\:\frac{\mathrm{1}}{−\mathrm{2}\:{e}^{−{i}\frac{\pi}{\mathrm{4}}} \:−\mathrm{4}\:{e}^{−{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \:\:\:−\mathrm{6}\:{e}^{−{i}\frac{\mathrm{5}\pi}{\mathrm{4}}} } \\ $$$$=\:\:\frac{−\mathrm{1}}{\mathrm{2}\:{e}^{−{i}\frac{\pi}{\mathrm{4}}} \:\:+\mathrm{4}\:{e}^{−{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \:\:+\mathrm{6}\:{e}^{−{i}\frac{\mathrm{5}\pi}{\mathrm{4}}} }\:=\:\frac{−\mathrm{1}}{\mathrm{2}\:{e}^{−{i}\frac{\pi}{\mathrm{4}}} \:\:−\mathrm{4}\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \:−\mathrm{6}\:{e}^{−{i}\frac{\pi}{\mathrm{4}}} } \\ $$$$=\:\:\frac{−\mathrm{1}}{−\mathrm{4}\left(\:{e}^{{i}\frac{\pi}{\mathrm{4}}} \:\:+{e}^{−{i}\frac{\pi}{\mathrm{4}}} \right)}\:=\:\:\frac{\mathrm{1}}{\mathrm{4}\:.\mathrm{2}.\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:\:=\mathrm{2}{i}\pi\left(\:\:\frac{\mathrm{1}}{\mathrm{4}{i}}\:\:−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\:+\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\right)\:=\:\frac{\pi}{\mathrm{2}}\:\:\Rightarrow \\ $$$${I}\:=\:\frac{\pi}{\mathrm{4}}\:. \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 13/Apr/18
another method the ch.x =(1/t) give I = −∫_0 ^∞ (1/((1+(1/t^2 ))(1+(1/t^4 )))) ((−dt)/t^2 ) = ∫_0 ^∞ (( t^4 dt)/((1+t^2 )(1+t^4 ))) =∫_0 ^∞ ((1+t^4 −1)/((1+t^2 )(1+t^4 )))dt = ∫_0 ^∞ (dt/(1+t^2 )) −∫_0 ^∞ (dt/((1+t^2 )(1+t^4 ))) =(π/2) −I⇒ 2I =(π/2) ⇒ I = (π/4) ★ I=(π/4) ★
$${another}\:{method} \\ $$$${the}\:{ch}.{x}\:=\frac{\mathrm{1}}{{t}}\:{give}\: \\ $$$${I}\:=\:−\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{4}} }\right)}\:\frac{−{dt}}{{t}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{\:{t}^{\mathrm{4}} {dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}+{t}^{\mathrm{4}} \:−\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:−\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{4}} \right)}\:=\frac{\pi}{\mathrm{2}}\:−{I}\Rightarrow \\ $$$$\mathrm{2}{I}\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow\:{I}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$\bigstar\:{I}=\frac{\pi}{\mathrm{4}}\:\bigstar \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *