Question Number 35440 by prof Abdo imad last updated on 19/May/18
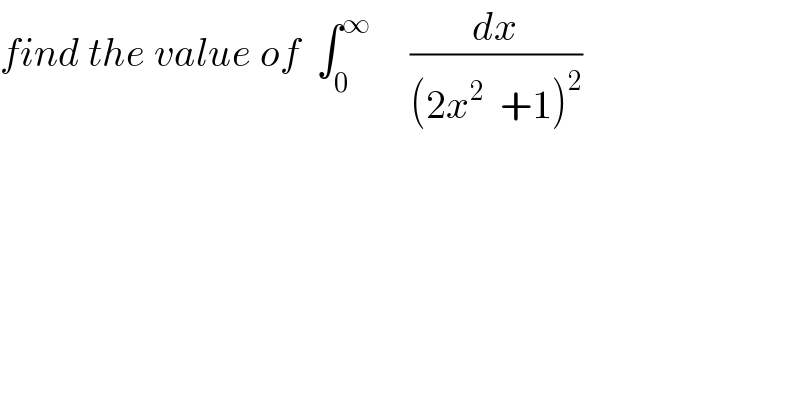
$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{2}{x}^{\mathrm{2}} \:\:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by prof Abdo imad last updated on 19/May/18

$${let}\:{put}\:{I}\:\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}{I}\:\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${let}\:{condider}\:{tbe}\:{complex}\:{function} \\ $$$$\varphi\left({z}\right)\:=\:\:\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\:{we}\:{have} \\ $$$$\varphi\left({z}\right)\:=\:\:\frac{\mathrm{1}}{\left({z}−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \left({z}\:+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }\:{so}\:{the}?{polrs}\:{of}\:\varphi\:{are} \\ $$$$\frac{{i}}{\:\sqrt{\mathrm{2}}}\:{and}\:\frac{−{i}}{\:\sqrt{\mathrm{2}}}\:\left({doubles}\right)\:{and}\:{Residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,\frac{{i}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$${Res}\left(\varphi,\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\:={lim}_{{z}\rightarrow\frac{{i}}{\:\sqrt{\mathrm{2}}}} \:\:\left\{\:\left({z}−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \varphi\left({z}\right)\right\}^{'} \\ $$$$={lim}_{{z}\rightarrow\frac{{i}}{\:\sqrt{\mathrm{2}}}} \:\:\:\left\{\:\left({z}+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)^{−\mathrm{2}} \right\}^{'} \\ $$$$={lim}_{{z}\rightarrow\frac{{i}}{\:\sqrt{\mathrm{2}}}} \:\:\:−\mathrm{2}\left({z}\:+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)^{−\mathrm{3}} \\ $$$$=−\mathrm{2}\:\left(\frac{\mathrm{2}{i}}{\:\sqrt{\mathrm{2}}}\right)^{−\mathrm{3}} \:=−\mathrm{2}\left(\sqrt{\mathrm{2}}\:{i}\right)^{−\mathrm{3}} =\mathrm{2}\:\left(\sqrt{\mathrm{2}}\right)^{−\mathrm{3}} .\frac{\mathrm{1}}{{i}} \\ $$$$=\:\frac{\mathrm{1}}{{i}\sqrt{\mathrm{2}}}\:\Rightarrow\:\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\:\frac{\mathrm{1}}{{i}\sqrt{\mathrm{2}}}\:=\:\pi\sqrt{\mathrm{2}} \\ $$$$\mathrm{2}{I}\:\:=\frac{\mathrm{1}}{\mathrm{4}}\:\pi\sqrt{\mathrm{2}}\:\:\Rightarrow\:{I}\:=\:\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}\:=\:\frac{\mathrm{2}\pi}{\mathrm{8}\sqrt{\mathrm{2}}}\:\Rightarrow\: \\ $$$${I}\:=\:\:\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\:. \\ $$
Commented by prof Abdo imad last updated on 19/May/18
![I = ∫_0 ^∞ (dx/((2x^2 +1)^2 )) let use the changement x=(1/( (√2))) tant ⇒ I = (1/( (√2)))∫_0 ^(π/2) ((1+tan^2 t)/((1+tan^2 )^2 ))dt = (1/( (√2))) ∫_0 ^(π/2) (dt/(1+tan^2 t)) = (1/( (√2))) ∫_0 ^(π/2) cos^2 t dt =(1/( (√2))) ∫_0 ^(π/2) (((1+cos(2t))/2))dt = (1/(2(√2))) (π/2) + (1/(4(√2)))[ sin(2t)]_0 ^(π/2) ★ I = (π/(4(√2))) ★](https://www.tinkutara.com/question/Q35501.png)
$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\:{let}\:{use}\:{the}\:{changement} \\ $$$${x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{tant}\:\Rightarrow\:{I}\:\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{tan}^{\mathrm{2}} {t}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{dt}}{\mathrm{1}+{tan}^{\mathrm{2}} {t}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{cos}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right){dt} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\:\frac{\pi}{\mathrm{2}}\:\:+\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[\:{sin}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\bigstar\:\:\:{I}\:=\:\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\bigstar \\ $$
Answered by ajfour last updated on 19/May/18
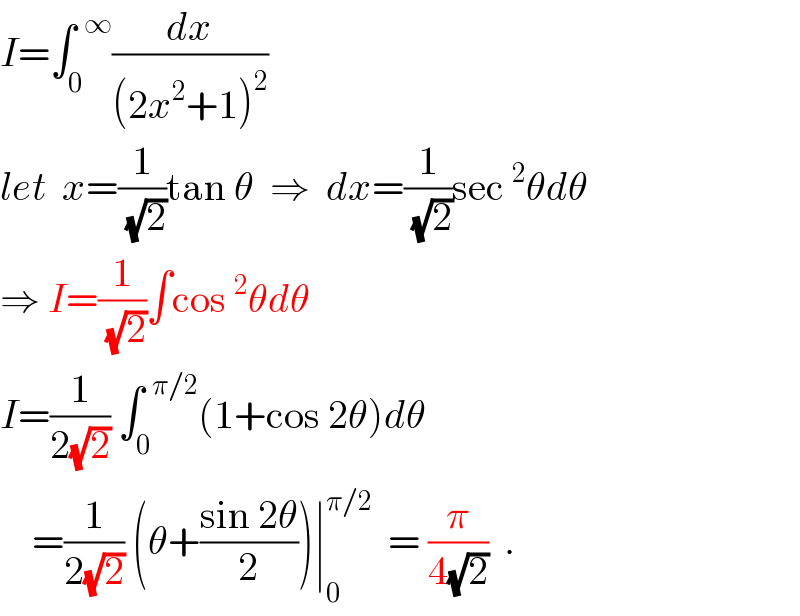
$${I}=\int_{\mathrm{0}} ^{\:\:\infty} \frac{{dx}}{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${let}\:\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}\:\theta\:\:\Rightarrow\:\:{dx}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta \\ $$$$\Rightarrow\:{I}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\mathrm{cos}\:^{\mathrm{2}} \theta{d}\theta \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right){d}\theta \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\left(\theta+\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}\right)\mid_{\mathrm{0}} ^{\pi/\mathrm{2}} \:\:=\:\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\:. \\ $$
