Question Number 26362 by abdo imad last updated on 24/Dec/17
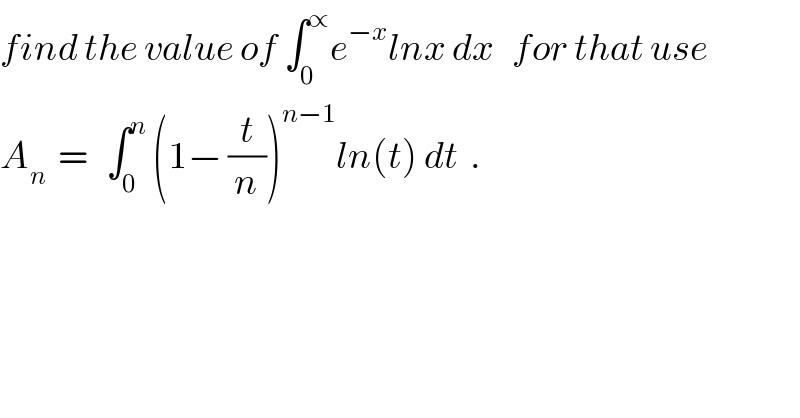
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\propto} {e}^{−{x}} {lnx}\:{dx}\:\:\:{for}\:{that}\:{use} \\ $$$${A}_{{n}} \:\:=\:\:\:\int_{\mathrm{0}} ^{{n}} \:\left(\mathrm{1}−\:\frac{{t}}{{n}}\right)^{{n}−\mathrm{1}} {ln}\left({t}\right)\:{dt}\:\:. \\ $$
