find-the-value-of-0-ln-1-t-2-1-t-2-dt-

Question Number 27181 by abdo imad last updated on 02/Jan/18

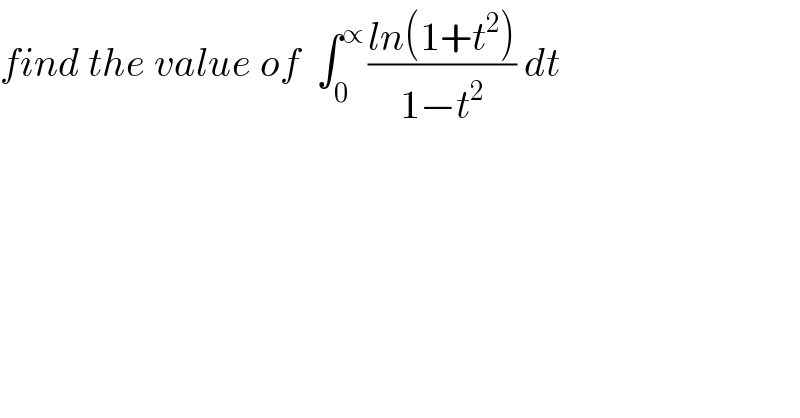
f i n d t h e v a l u e o f \int_{0}^{\propto} \frac{l n (1 + t^{2})}{1 - t^{2}} d t

Commented by abdo imad last updated on 08/Jan/18

l e t u s e t h e c h . t = \frac{1}{x}

I = - \int_{0}^{\infty} \frac{l n (1 + \frac{1}{x^{2}})}{1 - \frac{1}{x^{2}}} \frac{- d x}{x^{2}}

= \int_{0}^{\infty} \frac{l n (1 + x^{2}) - 2 l n x}{x^{2} - 1} d x

= - \int_{0}^{\infty} \frac{l n (1 + x^{2})}{1 - x^{2}} d x + 2 \int_{0}^{\infty} \frac{l n x}{1 - x^{2}} d x

\Rightarrow 2 I = 2 \int_{0}^{\infty} \frac{l n x}{1 - x^{2}} d x

\Rightarrow I = \int_{0}^{\infty} \frac{l n x}{1 - x^{2}} d x = \int_{0}^{1} \frac{l n x}{1 - x^{2}} + \int_{1}^{\propto} \frac{l n x}{1 - x^{2}} d x

t h e c h . x = \frac{1}{u} g i v e

\int_{1}^{\propto} \frac{l n x}{1 - x^{2}} d x = - \int_{0}^{1} \frac{- l n u}{1 - \frac{1}{u^{2}}} \frac{- d u}{u^{2}}

= - \int_{0}^{1} \frac{l n u}{u^{2} - 1} d u = \int_{0}^{1} \frac{l n u}{1 - u^{2}} d u

\Rightarrow I = 2 \int_{0}^{1} \frac{l n x}{1 - x^{2}} d x

I = 2 \int_{0}^{1} (\sum_{n = 0}^{\propto} x^{2 n}) l n x d x

I = 2 \sum_{n = 0}^{\propto} \int_{0}^{1} x^{2 n} l n x d x i n t r g r s t i o n b y p s r t s

\int_{0}^{1} x^{2 n} l n x d x = {[\frac{1}{2 n + 1} x^{2 n + 1} l n x]}_{0}^{1} - {\int^{1}}_{0} \frac{x^{2 n}}{2 n + 1} d x

= - \frac{1}{{(2 n + 1)}^{2}}

I = - 2 \sum_{n = 0}^{\propto} \frac{1}{{(2 n + 1)}^{2}} = - 2 . \frac{π^{2}}{8}

I = - \frac{π^{2}}{4} .