find-the-value-of-0-ln-t-3-t-2-1-t-dt-

Question Number 42506 by maxmathsup by imad last updated on 26/Aug/18

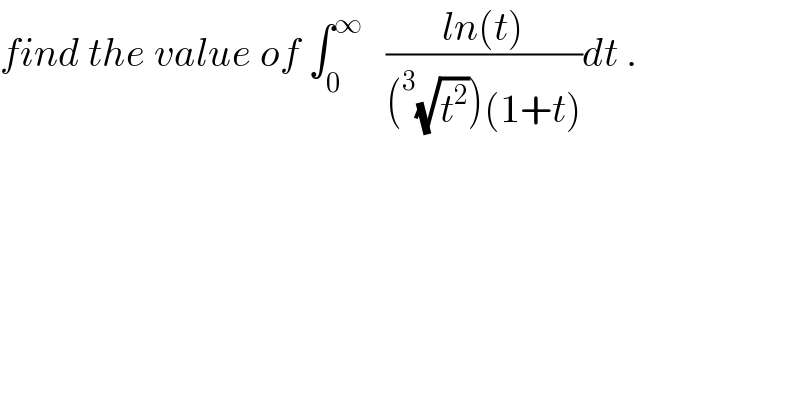
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({t}\right)}{\left(^{\mathrm{3}} \sqrt{{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+{t}\right)}{dt}\:. \\ $$

Commented by maxmathsup by imad last updated on 29/Aug/18

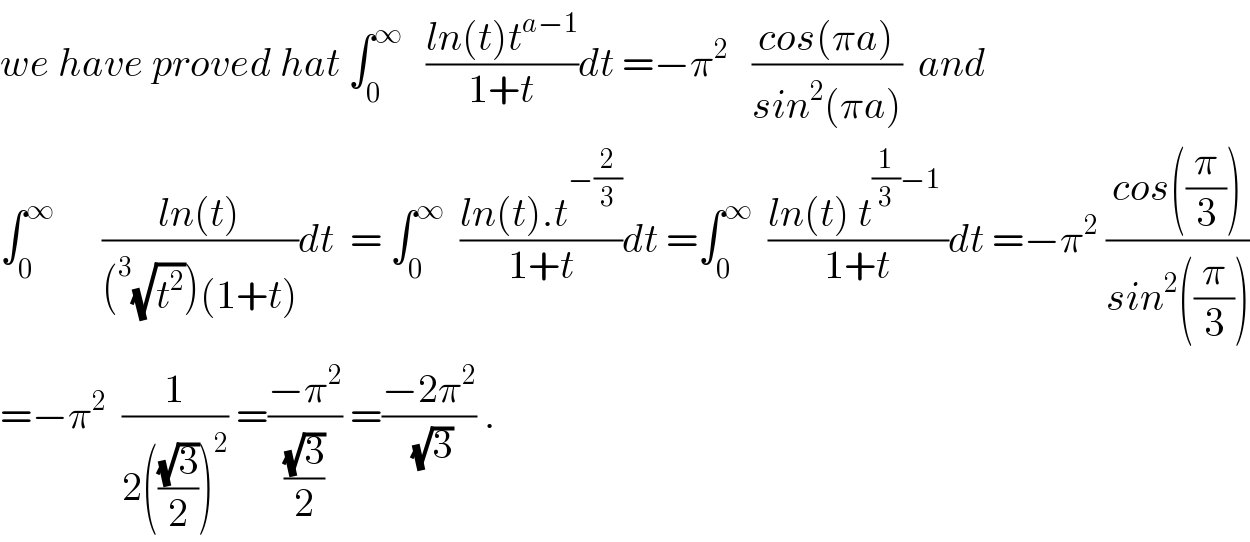
we have proved hat ∫_0 ^∞ ((ln(t)t^(a−1) )/(1+t))dt =−π^2 ((cos(πa))/(sin^2 (πa))) and ∫_0 ^∞ ((ln(t))/((^3 (√t^2 ))(1+t)))dt = ∫_0 ^∞ ((ln(t).t^(−(2/3)) )/(1+t))dt =∫_0 ^∞ ((ln(t) t^((1/3)−1) )/(1+t))dt =−π^2 ((cos((π/3)))/(sin^2 ((π/3)))) =−π^2 (1/(2(((√3)/2))^2 )) =((−π^2 )/((√3)/2)) =((−2π^2 )/( (√3))) .

$${we}\:{have}\:{proved}\:{hat}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({t}\right){t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=−\pi^{\mathrm{2}} \:\:\:\frac{{cos}\left(\pi{a}\right)}{{sin}^{\mathrm{2}} \left(\pi{a}\right)}\:\:{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{ln}\left({t}\right)}{\left(^{\mathrm{3}} \sqrt{{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+{t}\right)}{dt}\:\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({t}\right).{t}^{−\frac{\mathrm{2}}{\mathrm{3}}} }{\mathrm{1}+{t}}{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({t}\right)\:{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:}{\mathrm{1}+{t}}{dt}\:=−\pi^{\mathrm{2}} \:\frac{{cos}\left(\frac{\pi}{\mathrm{3}}\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{3}}\right)} \\ $$$$=−\pi^{\mathrm{2}} \:\:\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\frac{−\pi^{\mathrm{2}} }{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{−\mathrm{2}\pi^{\mathrm{2}} }{\:\sqrt{\mathrm{3}}}\:. \\ $$

Facebook Tweet Pin

find-the-value-of-0-ln-t-3-t-2-1-t-dt-

Leave a Reply Cancel reply