Menu Close

find-the-value-of-0-pi-4-cosx-sinx-tanx-dx-

Tinku Tara 0 Comments
Pin




Question Number 36057 by abdo mathsup 649 cc last updated on 28/May/18
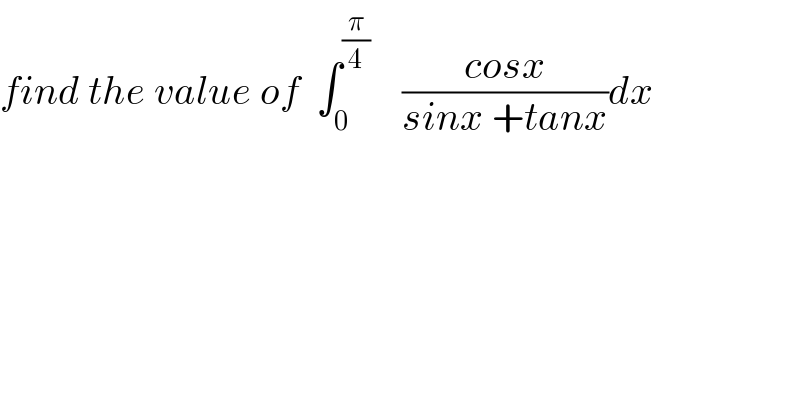
find the value of ∫_0 ^(π/4) ((cosx)/(sinx +tanx))dx
$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{cosx}}{{sinx}\:+{tanx}}{dx}\: \\ $$
Commented by abdo mathsup 649 cc last updated on 30/May/18
let I = ∫_0 ^(π/4) ((cosx)/(sinx +tanx))dx I = ∫_0 ^(π/4) ((cosx)/(sinx +((sinx)/(cosx))))dx = ∫_0 ^(π/4) ((cos^2 x)/(sinx.cosx +sinx))dx changement tan((x/2)) =t give I = ∫_0 ^((√2) −1) (((((1−t^2 )/(1+t^2 )))^2 )/(((2t (1−t^(2)) )/((1+t^2 )^2 )) +((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) = 2∫_0 ^((√2) −1) (((1−t^2 )^2 )/(2t(1−t^2 ) +2t(1+t^2 ))) (dt/(1+t^2 )) =2 ∫_0 ^((√2) −1) (((1−t^2 )^2 )/((1+t^2 )( 2t −2t^3 +2t +2t^3 )))dt = (1/2) ∫_0 ^((√2) −1) (((1−t^2 )^2 )/((1+t^2 )t)) dt ⇒ 2I = ∫_0 ^((√2)−1) ((t^4 −2t^2 +1)/(t^3 +t))dt =∫_0 ^((√2)−1) ((t(t^3 +t)−t^2 −2t^2 +1)/(t^(3 ) +t))dt = ∫_0 ^((√2)−1) t dt +∫_0 ^((√2) −1) ((−3t^2 +1)/(t^3 +t))dt but ∫_0 ^((√2) −1) tdt =[(t^2 /2)]_0 ^((√2)−1) =((((√2)−1)^2 )/2) let decompose F(t) = ((−3t^2 +1)/(t^3 +t)) F(t) = ((−3t^2 +1)/(t^3 +t)) = (a/t) +((bt +c)/(t^2 +1)) a=lim_(t→0) tF(t) = 1 =a lim_(t→+∞) t F(t) = −3 =a +b ⇒b=−3−a=−4 F(t) = (1/t) +((−4t +c)/(t^(2 ) +1)) F(1) =−1 = 1 +((−4+c)/2) =−1 +(c/2) ⇒c=0 ⇒ F(t)= (1/t) −((4t)/(t^2 +1)) ⇒ ∫_0 ^((√2) −1) ((−3t^2 +1)/(t^3 +t))dt = ∫_0 ^((√2)−1) { (1/t) −((4t)/(t^2 +1))}dt =[ln∣t∣ −2 ln(t^2 +1)]_0 ^((√2) −1) = [ln( (t/((t^2 +1)^2 )))]_0 ^((√2)−1) = ln((((√2) −1)/({((√2) −1)^2 +1}^( ))) −ln(0^+ ) =+∞ so this integral is divergent !
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{cosx}}{{sinx}\:+{tanx}}{dx} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{cosx}}{{sinx}\:+\frac{{sinx}}{{cosx}}}{dx}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{cos}^{\mathrm{2}} {x}}{{sinx}.{cosx}\:+{sinx}}{dx} \\ $$$${changement}\:\:\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)\:={t}\:{give} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\:\:\frac{\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }{\frac{\mathrm{2}{t}\:\left(\mathrm{1}−{t}^{\left.\mathrm{2}\right)} \right.}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\:+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\:\:\:\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\:+\mathrm{2}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\:\:\:\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\:\mathrm{2}{t}\:−\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}\:+\mathrm{2}{t}^{\mathrm{3}} \right)}{dt} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\:\:\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right){t}}\:{dt}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\frac{{t}^{\mathrm{4}} \:−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{3}} \:+{t}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\frac{{t}\left({t}^{\mathrm{3}} +{t}\right)−{t}^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{3}\:} +{t}}{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:{t}\:{dt}\:\:+\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\frac{−\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{3}} \:+{t}}{dt}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} {tdt}\:=\left[\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:=\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\:\:{let}\:{decompose} \\ $$$${F}\left({t}\right)\:=\:\frac{−\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{3}} +{t}} \\ $$$${F}\left({t}\right)\:=\:\frac{−\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{3}} \:+{t}}\:=\:\frac{{a}}{{t}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}={lim}_{{t}\rightarrow\mathrm{0}} {tF}\left({t}\right)\:=\:\mathrm{1}\:={a} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\:{F}\left({t}\right)\:=\:−\mathrm{3}\:={a}\:+{b}\:\Rightarrow{b}=−\mathrm{3}−{a}=−\mathrm{4} \\ $$$${F}\left({t}\right)\:=\:\:\frac{\mathrm{1}}{{t}}\:+\frac{−\mathrm{4}{t}\:+{c}}{{t}^{\mathrm{2}\:} +\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=−\mathrm{1}\:=\:\mathrm{1}\:+\frac{−\mathrm{4}+{c}}{\mathrm{2}}\:=−\mathrm{1}\:+\frac{{c}}{\mathrm{2}}\:\Rightarrow{c}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({t}\right)=\:\frac{\mathrm{1}}{{t}}\:\:−\frac{\mathrm{4}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\frac{−\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{3}} \:\:+\mathrm{t}}\mathrm{dt}\:=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \left\{\:\frac{\mathrm{1}}{{t}}\:−\frac{\mathrm{4}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\right\}{dt} \\ $$$$=\left[{ln}\mid{t}\mid\:−\mathrm{2}\:{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \\ $$$$=\:\left[{ln}\left(\:\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:=\:{ln}\left(\frac{\sqrt{\mathrm{2}}\:−\mathrm{1}}{\left\{\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right\}^{\left(\right.} }\right)\:−{ln}\left(\mathrm{0}^{+} \right) \\ $$$$=+\infty\:\:{so}\:{this}\:{integral}\:{is}\:{divergent}\:! \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/May/18
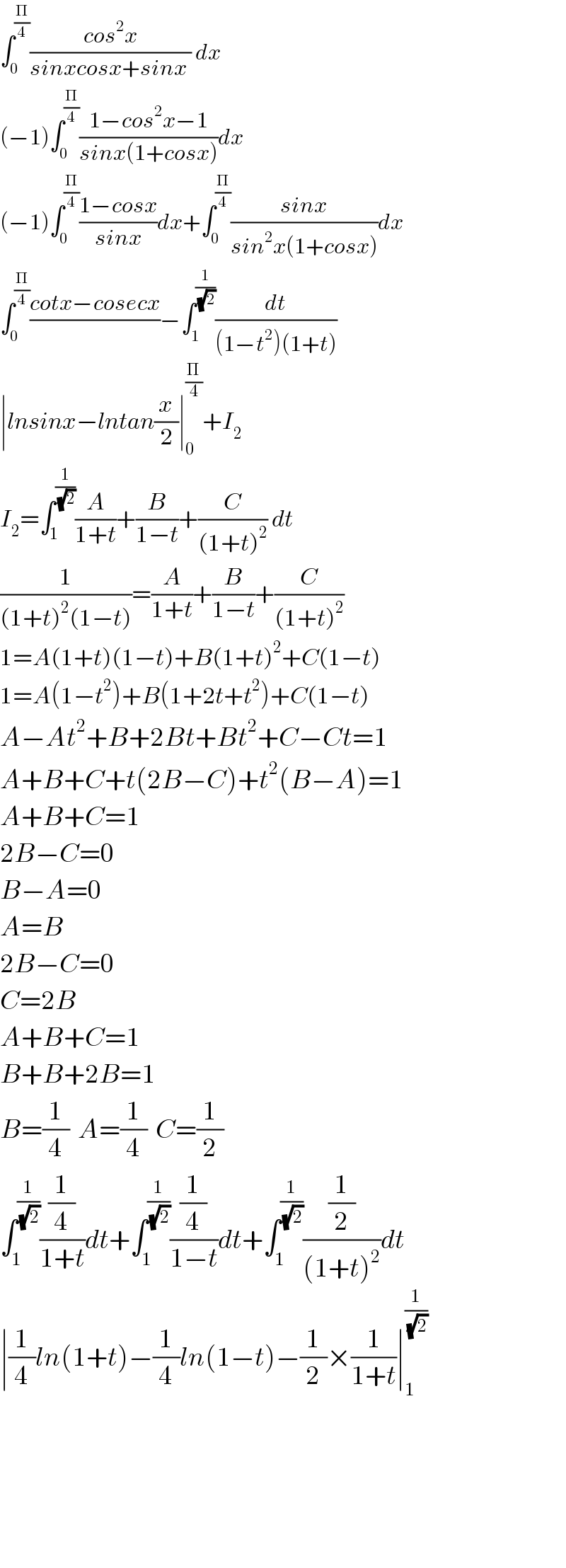
∫_0 ^(Π/4) ((cos^2 x)/(sinxcosx+sinx )) dx (−1)∫_0 ^(Π/4) ((1−cos^2 x−1)/(sinx(1+cosx)))dx (−1)∫_0 ^(Π/4) ((1−cosx)/(sinx))dx+∫_0 ^(Π/4) ((sinx)/(sin^2 x(1+cosx)))dx ∫_0 ^(Π/4) ((cotx−cosecx)/)−∫_1 ^(1/( (√2))) (dt/((1−t^2 )(1+t))) ∣lnsinx−lntan(x/2)∣_0 ^(Π/4) +I_2 I_2 =∫_1 ^(1/( (√2))) (A/(1+t))+(B/(1−t))+(C/((1+t)^2 )) dt (1/((1+t)^2 (1−t)))=(A/(1+t))+(B/(1−t))+(C/((1+t)^2 )) 1=A(1+t)(1−t)+B(1+t)^2 +C(1−t) 1=A(1−t^2 )+B(1+2t+t^2 )+C(1−t) A−At^2 +B+2Bt+Bt^2 +C−Ct=1 A+B+C+t(2B−C)+t^2 (B−A)=1 A+B+C=1 2B−C=0 B−A=0 A=B 2B−C=0 C=2B A+B+C=1 B+B+2B=1 B=(1/4) A=(1/4) C=(1/2) ∫_1 ^(1/( (√2))) ((1/4)/(1+t))dt+∫_1 ^(1/( (√2))) ((1/4)/(1−t))dt+∫_1 ^(1/( (√2))) ((1/2)/((1+t)^2 ))dt ∣(1/4)ln(1+t)−(1/4)ln(1−t)−(1/2)×(1/(1+t))∣_1 ^(1/( (√2)))
$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{cos}^{\mathrm{2}} {x}}{{sinxcosx}+{sinx}\:}\:{dx} \\ $$$$\left(−\mathrm{1}\right)\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{\mathrm{1}−{cos}^{\mathrm{2}} {x}−\mathrm{1}}{{sinx}\left(\mathrm{1}+{cosx}\right)}{dx} \\ $$$$\left(−\mathrm{1}\right)\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{\mathrm{1}−{cosx}}{{sinx}}{dx}+\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{sinx}}{{sin}^{\mathrm{2}} {x}\left(\mathrm{1}+{cosx}\right)}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{cotx}−{cosecx}}{}−\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{{dt}}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}\right)} \\ $$$$\mid{lnsinx}−{lntan}\frac{{x}}{\mathrm{2}}\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} +{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} =\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{{A}}{\mathrm{1}+{t}}+\frac{{B}}{\mathrm{1}−{t}}+\frac{{C}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\:{dt} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} \left(\mathrm{1}−{t}\right)}=\frac{{A}}{\mathrm{1}+{t}}+\frac{{B}}{\mathrm{1}−{t}}+\frac{{C}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} } \\ $$$$\mathrm{1}={A}\left(\mathrm{1}+{t}\right)\left(\mathrm{1}−{t}\right)+{B}\left(\mathrm{1}+{t}\right)^{\mathrm{2}} +{C}\left(\mathrm{1}−{t}\right) \\ $$$$\mathrm{1}={A}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+{B}\left(\mathrm{1}+\mathrm{2}{t}+{t}^{\mathrm{2}} \right)+{C}\left(\mathrm{1}−{t}\right) \\ $$$${A}−{At}^{\mathrm{2}} +{B}+\mathrm{2}{Bt}+{Bt}^{\mathrm{2}} +{C}−{Ct}=\mathrm{1} \\ $$$${A}+{B}+{C}+{t}\left(\mathrm{2}{B}−{C}\right)+{t}^{\mathrm{2}} \left({B}−{A}\right)=\mathrm{1} \\ $$$${A}+{B}+{C}=\mathrm{1} \\ $$$$\mathrm{2}{B}−{C}=\mathrm{0} \\ $$$${B}−{A}=\mathrm{0} \\ $$$${A}={B} \\ $$$$\mathrm{2}{B}−{C}=\mathrm{0} \\ $$$${C}=\mathrm{2}{B} \\ $$$${A}+{B}+{C}=\mathrm{1} \\ $$$${B}+{B}+\mathrm{2}{B}=\mathrm{1} \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{4}}\:\:{A}=\frac{\mathrm{1}}{\mathrm{4}}\:\:{C}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}+{t}}{dt}+\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}−{t}}{dt}+\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{\frac{\mathrm{1}}{\mathrm{2}}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$$\mid\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+{t}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}−{t}\right)−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{1}+{t}}\mid_{\mathrm{1}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by sma3l2996 last updated on 28/May/18
A=∫_0 ^(π/4) ((cosx)/(sinx+tanx))dx=∫_0 ^(π/4) ((cos^2 x)/(cosxsinx+sinx))dx =∫_0 ^(π/4) ((1−sin^2 x)/(sinx(cosx+1)))dx=∫_0 ^(π/4) (dx/(sinx(cosx+1)))−∫_0 ^(π/4) ((sinx)/(1+cosx))dx =∫_0 ^(π/4) (dx/(sinx(cosx+1)))+[ln∣1+cosx∣]_0 ^(π/4) let u=tanx/2⇒dx=((2du)/(1+u^2 )) sinx=2cos(x/2)sin(x/2)=((2u)/(1+u^2 )) 1+cosx=2cos^2 (x/2)=(2/(1+u^2 )) A=ln((((√2)+1)/2))−ln2+∫_0 ^(tan^(−1) (π/8)) (1/(((2u)/(1+u^2 ))×(2/(1+u^2 ))))×((2du)/(1+u^2 )) A=ln((√2)+2)−2ln2+(1/2)∫_0 ^((√2)−1) ((1+u^2 )/u)du =ln((√2)+2)−2ln2+(1/2)[lnu+(1/2)u^2 ]_0 ^((√2)−1) A=−∞ because (lim_(u→0) lnu=−∞)
$${A}=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{cosx}}{{sinx}+{tanx}}{dx}=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{cos}^{\mathrm{2}} {x}}{{cosxsinx}+{sinx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{\mathrm{1}−{sin}^{\mathrm{2}} {x}}{{sinx}\left({cosx}+\mathrm{1}\right)}{dx}=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{dx}}{{sinx}\left({cosx}+\mathrm{1}\right)}−\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{sinx}}{\mathrm{1}+{cosx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{{dx}}{{sinx}\left({cosx}+\mathrm{1}\right)}+\left[{ln}\mid\mathrm{1}+{cosx}\mid\right]_{\mathrm{0}} ^{\pi/\mathrm{4}} \\ $$$${let}\:\:{u}={tanx}/\mathrm{2}\Rightarrow{dx}=\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$${sinx}=\mathrm{2}{cos}\left({x}/\mathrm{2}\right){sin}\left({x}/\mathrm{2}\right)=\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$\mathrm{1}+{cosx}=\mathrm{2}{cos}^{\mathrm{2}} \left({x}/\mathrm{2}\right)=\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$${A}={ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{2}}\right)−{ln}\mathrm{2}+\int_{\mathrm{0}} ^{{tan}^{−\mathrm{1}} \left(\pi/\mathrm{8}\right)} \frac{\mathrm{1}}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }×\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} }}×\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$${A}={ln}\left(\sqrt{\mathrm{2}}+\mathrm{2}\right)−\mathrm{2}{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\mathrm{1}+{u}^{\mathrm{2}} }{{u}}{du} \\ $$$$={ln}\left(\sqrt{\mathrm{2}}+\mathrm{2}\right)−\mathrm{2}{ln}\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\left[{lnu}+\frac{\mathrm{1}}{\mathrm{2}}{u}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$${A}=−\infty\:\:\:\:{because}\:\left(\underset{{u}\rightarrow\mathrm{0}} {{lim}lnu}=−\infty\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *