Question Number 42391 by abdo.msup.com last updated on 24/Aug/18
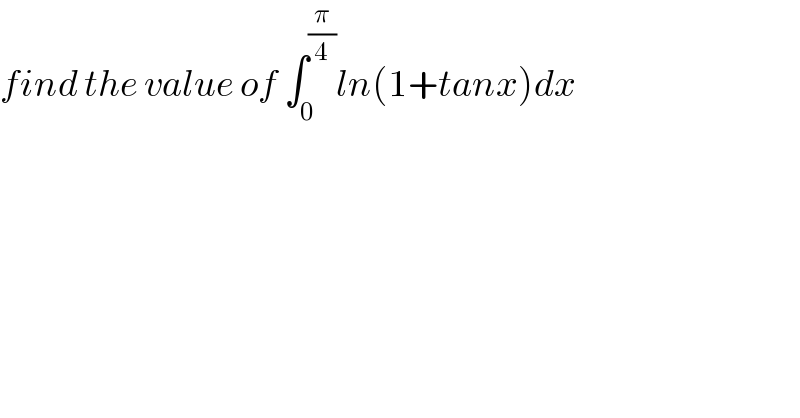
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tanx}\right){dx} \\ $$
Commented by maxmathsup by imad last updated on 25/Aug/18
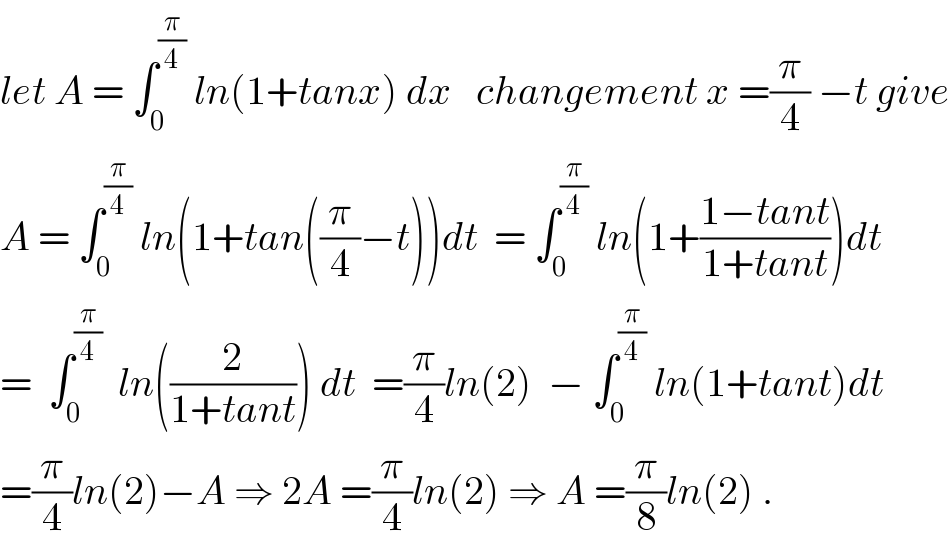
$${let}\:{A}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left(\mathrm{1}+{tanx}\right)\:{dx}\:\:\:{changement}\:{x}\:=\frac{\pi}{\mathrm{4}}\:−{t}\:{give} \\ $$$${A}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left(\mathrm{1}+{tan}\left(\frac{\pi}{\mathrm{4}}−{t}\right)\right){dt}\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left(\mathrm{1}+\frac{\mathrm{1}−{tant}}{\mathrm{1}+{tant}}\right){dt} \\ $$$$=\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:{ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tant}}\right)\:{dt}\:\:=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:\:−\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{ln}\left(\mathrm{1}+{tant}\right){dt} \\ $$$$=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)−{A}\:\Rightarrow\:\mathrm{2}{A}\:=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:\Rightarrow\:{A}\:=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Aug/18
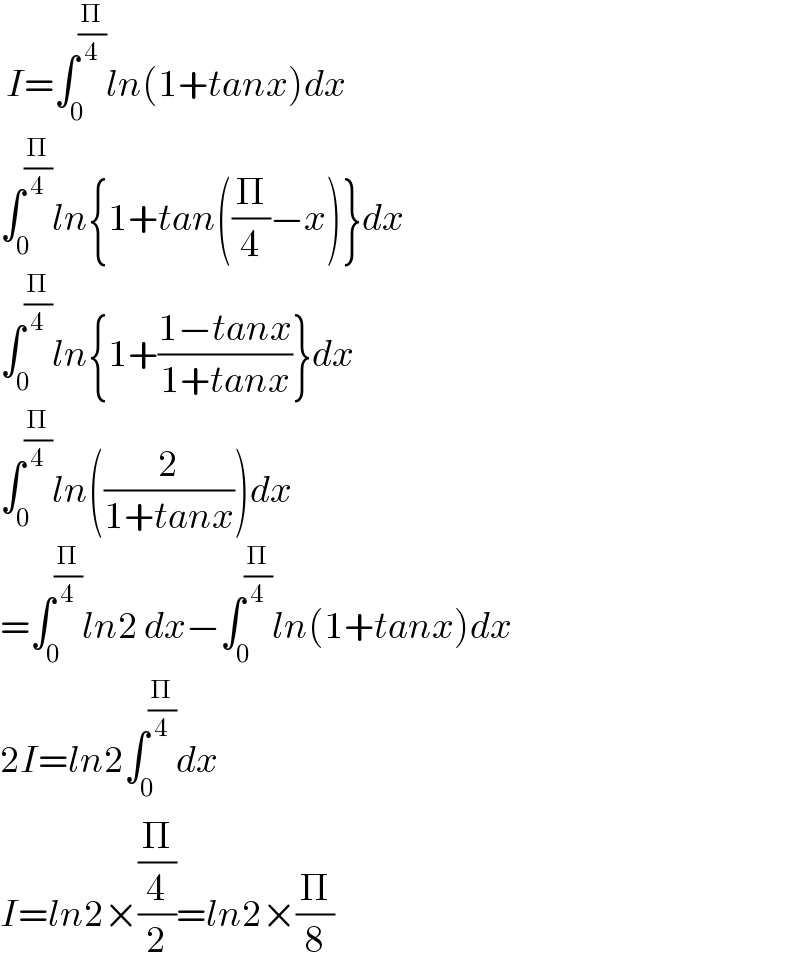
$$\:{I}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tanx}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\left\{\mathrm{1}+{tan}\left(\frac{\Pi}{\mathrm{4}}−{x}\right)\right\}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\left\{\mathrm{1}+\frac{\mathrm{1}−{tanx}}{\mathrm{1}+{tanx}}\right\}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tanx}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\mathrm{2}\:{dx}−\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tanx}\right){dx} \\ $$$$\mathrm{2}{I}={ln}\mathrm{2}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} {dx} \\ $$$${I}={ln}\mathrm{2}×\frac{\frac{\Pi}{\mathrm{4}}}{\mathrm{2}}={ln}\mathrm{2}×\frac{\Pi}{\mathrm{8}} \\ $$
