Menu Close

find-the-value-of-0-sin-x-2-x-4-4-dx-

Tinku Tara 0 Comments
Pin




Question Number 56698 by maxmathsup by imad last updated on 21/Mar/19
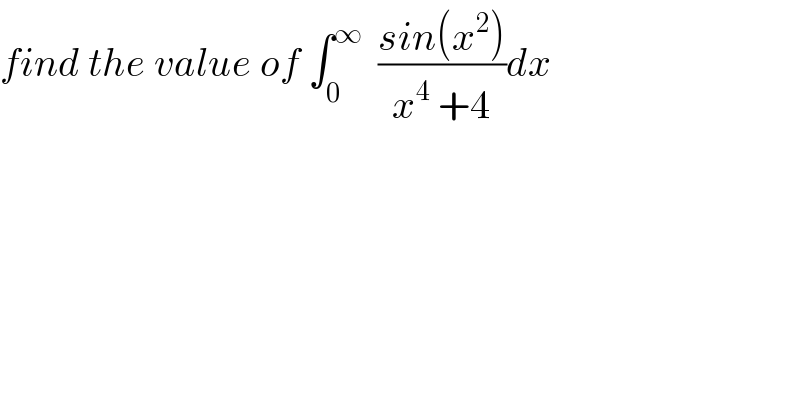
find the value of ∫_0 ^∞ ((sin(x^2 ))/(x^4 +4))dx
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{4}} \:+\mathrm{4}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 23/Mar/19
let A =∫_0 ^∞ ((sin(x^2 ))/(x^4 +4)) dx ⇒2A = ∫_(−∞) ^(+∞) ((sin(x^2 ))/(x^4 +4))dx =Im (∫_(−∞) ^(+∞) (e^(ix^2 ) /(x^4 +4))dx) let but ∫_(−∞) ^(+∞) (e^(ix^2 ) /(x^4 +4)) dx =_(x=(√2)t) ∫_(−∞) ^(+∞) (e^(i2t^2 ) /(4t^4 +4)) (√2)dt =((√2)/4) ∫_(−∞) ^(+∞) (e^(2it^2 ) /(t^4 +1)) dt let ϕ(z) = (e^(2iz^2 ) /(z^4 +1)) ⇒ϕ(z) =(e^(2iz^2 ) /((z^2 −i)(z^2 +i))) =(e^(2iz^2 ) /((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^(−((iπ)/4)) ))) so the poles of ϕ are +^− e^((iπ)/4) and +^− e^(−((iπ)/4)) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ, e^((iπ)/4) )+Res(ϕ,−e^(−((iπ)/4)) )} Res(ϕ,e^((iπ)/4) ) = (e^(2i(i)) /(2e^((iπ)/4) (2i))) =(e^(−2) /(4i)) e^(−((iπ)/4)) Res(ϕ,−e^(−((iπ)/4)) ) = (e^(2i(−i)) /(−2e^(−((iπ)/4)) (−2i))) =(e^2 /(4i)) e^((iπ)/4) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ {(e^(−2) /(4i)) e^(−((iπ)/4)) +(e^2 /(4i)) e^((iπ)/4) } =(π/2) { e^(−2) {(1/( (√2))) −(i/( (√2)))} +e^2 {(1/( (√2))) +(i/( (√2)))}} =(π/2){ (1/( (√2)))(e^2 +e^(−2) ) +(i/( (√2)))(e^2 −e^(−2) )} ⇒ 2A =(π/(2(√2)))(e^2 −e^(−2) ) ⇒ ★A =(π/(4(√2))) (e^2 −e^(−2) ) ★
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{4}} \:+\mathrm{4}}\:{dx}\:\Rightarrow\mathrm{2}{A}\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{4}} \:+\mathrm{4}}{dx}\:={Im}\:\left(\int_{−\infty} ^{+\infty} \:\frac{{e}^{{ix}^{\mathrm{2}} } }{{x}^{\mathrm{4}} \:+\mathrm{4}}{dx}\right)\:{let} \\ $$$${but}\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{ix}^{\mathrm{2}} } }{{x}^{\mathrm{4}} \:+\mathrm{4}}\:{dx}\:=_{{x}=\sqrt{\mathrm{2}}{t}} \:\:\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{i}\mathrm{2}{t}^{\mathrm{2}} } }{\mathrm{4}{t}^{\mathrm{4}} \:+\mathrm{4}}\:\sqrt{\mathrm{2}}{dt}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{\mathrm{2}{it}^{\mathrm{2}} } }{{t}^{\mathrm{4}} \:+\mathrm{1}}\:{dt}\:{let} \\ $$$$\varphi\left({z}\right)\:=\:\frac{{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{{z}^{\mathrm{4}} \:+\mathrm{1}}\:\Rightarrow\varphi\left({z}\right)\:=\frac{{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}^{\mathrm{2}} −{i}\right)\left({z}^{\mathrm{2}} \:+{i}\right)}\:=\frac{{e}^{\mathrm{2}{iz}^{\mathrm{2}} } }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$${so}\:{the}\:{poles}\:{of}\:\varphi\:{are}\:\overset{−} {+}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{and}\:\overset{−} {+}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\:{Res}\left(\varphi,\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:=\:\frac{{e}^{\mathrm{2}{i}\left({i}\right)} }{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{2}{i}\right)}\:=\frac{{e}^{−\mathrm{2}} }{\mathrm{4}{i}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:=\:\frac{{e}^{\mathrm{2}{i}\left(−{i}\right)} }{−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \left(−\mathrm{2}{i}\right)}\:=\frac{{e}^{\mathrm{2}} }{\mathrm{4}{i}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\frac{{e}^{−\mathrm{2}} }{\mathrm{4}{i}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:+\frac{{e}^{\mathrm{2}} }{\mathrm{4}{i}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right\}\:=\frac{\pi}{\mathrm{2}}\:\left\{\:{e}^{−\mathrm{2}} \left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right\}\:+{e}^{\mathrm{2}} \left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right\}\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\left\{\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left({e}^{\mathrm{2}} \:+{e}^{−\mathrm{2}} \right)\:+\frac{{i}}{\:\sqrt{\mathrm{2}}}\left({e}^{\mathrm{2}} \:−{e}^{−\mathrm{2}} \right)\right\}\:\Rightarrow\:\mathrm{2}{A}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\left({e}^{\mathrm{2}} −{e}^{−\mathrm{2}} \right)\:\:\Rightarrow \\ $$$$\bigstar{A}\:=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\left({e}^{\mathrm{2}} \:−{e}^{−\mathrm{2}} \right)\:\bigstar \\ $$
Commented by maxmathsup by imad last updated on 23/Mar/19
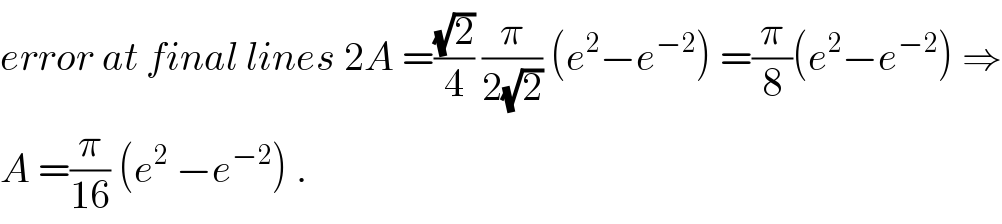
error at final lines 2A =((√2)/4) (π/(2(√2))) (e^2 −e^(−2) ) =(π/8)(e^2 −e^(−2) ) ⇒ A =(π/(16)) (e^2 −e^(−2) ) .
$${error}\:{at}\:{final}\:{lines}\:\mathrm{2}{A}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:\left({e}^{\mathrm{2}} −{e}^{−\mathrm{2}} \right)\:=\frac{\pi}{\mathrm{8}}\left({e}^{\mathrm{2}} −{e}^{−\mathrm{2}} \right)\:\Rightarrow \\ $$$${A}\:=\frac{\pi}{\mathrm{16}}\:\left({e}^{\mathrm{2}} \:−{e}^{−\mathrm{2}} \right)\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *